
LA MIA MATEMATICA
A) GEOMETRIA
1) Nuovi Teoremi sul Triangolo Rettangolo
2) Risoluzione algebrica del teorema di Pitagora
3) Teoremi geometrici al posto di Equazioni di II grado
4) Teorema sulle proiezioni dei cateti
5) Come ottenere le Terne Pitagoriche Primitive e multiple
6) Terne pitagoriche entro il 1000
B) ARITMETICA
7) I Numeri Primi
8) Dai multipli del 6 ai Numeri Primi
9) Sui Quadrati dei Numeri Interi
10) Sui Cubi dei Numeri Interi
11) Il Mediano e i suoi Simmetrici
12) Radice dei Quadrati dei Numeri da 11 a 99
13) Radice dei Cubi dei Numeri da 11 a 99
14) Moltiplicazioni dirette mediante il grafico
15) Moltiplicazioni per 11
16) Nuovo Sistema Numerico in Lettere
17) I Numeri: dalle unità ai Miliardi
18) Numeri oltre i Miliardi
19) Nomi dei Multipli e dei Sottomultipli delle Potenze del 10
20) unità Fondamentali di Misura e loro Simboli
21) Sistema Metrico Decimale
22) Tabella delle potenze del 10 fino all'esponente 1000
_______________________________________________________
A) GEOMETRIA
1) Nuovi teoremi sul triangolo rettangolo
Teorema 1
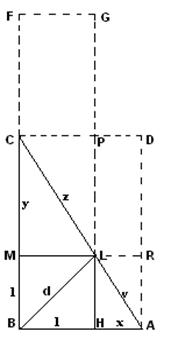
Il rettangolo costruito sui cateti AB e BC, ossia ABCD, è equivalente al rettangolo costruito sulla somma dei cateti BF e il lato del quadrato BH, ossia BFGH. Per cui, indicando con a e b il cateto maggiore e quello minore, con l il lato e con d la diagonale del quadrato o bisettrice del triangolo rettangolo, avremo:
ABCD ~ BFGH; da cui:
![]()
PROBLEMI
Nel triangolo rettangolo ABC, i cateti BC (a) e BA (b) misurano rispettivamente 28 cm e 21 cm. Calcolare il lato del quadrato inscritto l e la
diagonale d.
![]()
Nel triangolo rettangolo ABC, l'area misura 294 cm² e il lato del quadrato misura 12 cm. Calcolare la somma dei cateti.
![]()
Nel triangolo rettangolo ABC, la somma dei cateti misura 49 cm e il lato del quadrato misura 12 cm. Calcolare l'area.
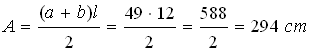 quadrati
quadrati
Nel triangolo rettangolo ABC, la somma dei cateti misura 49 cm e l'area misura 294 cm². Calcolare il lato del quadrato e la sua diagonale.
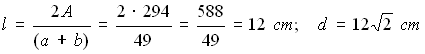
Teorema 2
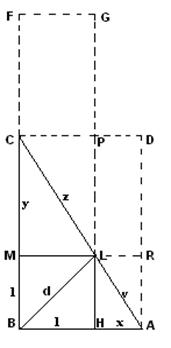 Il
rettangolo costruito sulle differenze tra ogni cateto e il lato del quadrato,
ossia LRDP, è equivalente al quadrato inscritto nel triangolo, ossia
BHLM. Ciò vuol dire che il lato del quadrato è medio proporzionale tra tali
differenze AH e CM. Per cui, indicandole con x (la minore)
e con y (la maggiore), avremo:
Il
rettangolo costruito sulle differenze tra ogni cateto e il lato del quadrato,
ossia LRDP, è equivalente al quadrato inscritto nel triangolo, ossia
BHLM. Ciò vuol dire che il lato del quadrato è medio proporzionale tra tali
differenze AH e CM. Per cui, indicandole con x (la minore)
e con y (la maggiore), avremo:
LRDP ~ BHLM; da cui:
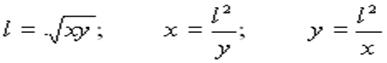
PROBLEMI
Nel triangolo rettangolo ABC, x e y misurano rispettivamente 9 cm e 16 cm. Calcolare il lato del quadrato inscritto.
![]()
Nel triangolo rettangolo ABC, il lato del quadrato misura 12 cm e y misura 16
cm. Calcolare la misura di x.
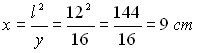
Nel triangolo rettangolo ABC, il lato del quadrato misura 12 cm e x misura 9 cm.
Calcolare la misura di y.
![]()
Teorema 3
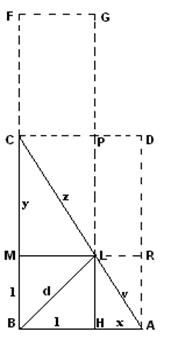
Il rettangolo costruito sulla somma dei cateti (BC+ BA) e la somma delle loro differenze (HA+MC) ` equivalente al quadrato costruito sull'ipotenusa AC. Ciò vuol dire che l'ipotenusa è media proporzionale tra tali somme. Per cui, indicando con a e b il cateto maggiore e quello minore, con c l'ipotenusa, con x e y rispettivamente la differenza minore e quella maggiore, avremo:
BC+BA) (AH+CM) ~ AC AC; da cui:
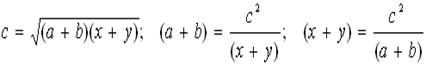
PROBLEMI
Nel triangolo rettangolo ABC, i cateti misurano 28 cm e 21 cm, mentre y e x
misurano rispettivamente 16 cm e 9 cm. Calcolare l'ipotenusa.
![]()
Nel triangolo ABC, l'ipotenusa misura cm 35, mentre la somma di y + x misura 25
cm. Calcolare la somma dei cateti.
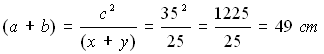
Nel triangolo ABC, l'ipotenusa misura cm 35, mentre la somma dei cateti misura
49 cm. Calcolare la somma di y + x.
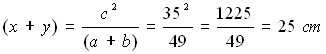
Teorema 4
 Il
quadrato di ciascun cateto è equivalente al rettangolo costruito sulla somma dei
cateti BC+BA e la relativa differenza AH o CM. Per
cui, indicando con a e b rispettivamente il cateto maggiore e
quello minore, con c l'ipotenusa, con x e y la differenza
minore e quella maggiore, avremo:
Il
quadrato di ciascun cateto è equivalente al rettangolo costruito sulla somma dei
cateti BC+BA e la relativa differenza AH o CM. Per
cui, indicando con a e b rispettivamente il cateto maggiore e
quello minore, con c l'ipotenusa, con x e y la differenza
minore e quella maggiore, avremo:
(BC+BA) MC ~ BC ; da cui:
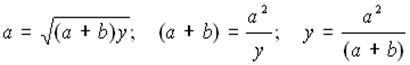
PROBLEMA
Nel triangolo rettangolo ABC, i cateti a e b misurano rispettivamente 28 cm e 21 cm. Calcolare le misure di x e di y.
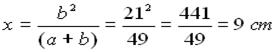
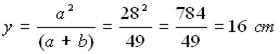
Teorema 5
 Ogni
cateto è medio proporzionale tra la somma dei cateti e la relativa differenza.
Per cui, indicando con a e b il cateto maggiore e quello minore, con x e y la
differenza minore e quella maggiore, avremo:
Ogni
cateto è medio proporzionale tra la somma dei cateti e la relativa differenza.
Per cui, indicando con a e b il cateto maggiore e quello minore, con x e y la
differenza minore e quella maggiore, avremo:
(BC+BA) HA ~ BA ; da cui:
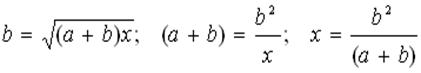
PROBLEMA
Nel triangolo rettangolo ABC, la somma dei cateti misura 49 cm, mentre y e x
misurano rispettivamente 16 cm e 9 cm. Calcolare i cateti.
![]()
![]()
Teorema 6
 Il
rettangolo costruito sul cateto maggiore, ossia BC, e l'ipotenusa AC
è equivalente al rettangolo costruito sulla somma dei cateti BC+BA
e la parte minore dell'ipotenusa che viene divisa dalla bisettrice, ossia LA.
Per cui, indicando con a e b il cateto maggiore e quello minore,
con c l'ipotenusa e con z il segmento maggiore dell'ipotenusa,
avremo:
Il
rettangolo costruito sul cateto maggiore, ossia BC, e l'ipotenusa AC
è equivalente al rettangolo costruito sulla somma dei cateti BC+BA
e la parte minore dell'ipotenusa che viene divisa dalla bisettrice, ossia LA.
Per cui, indicando con a e b il cateto maggiore e quello minore,
con c l'ipotenusa e con z il segmento maggiore dell'ipotenusa,
avremo:
BA AC ~ (BC+BA) LA; da cui:
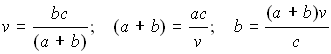
PROBLEMI
Nel triangolo rettangolo ABC, i cateti a e b misurano rispettivamente 28 cm e 21 cm, mentre l'ipotenusa misura 35 cm. Calcolare la misura di v.
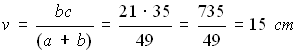
Nel triangolo rettangolo ABC, la somma dei cateti misura 49 cm, l'ipotenusa misura 35 cm, mentre v misura 15 cm. Calcolare il cateto minore.
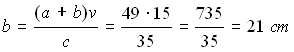
Teorema 7
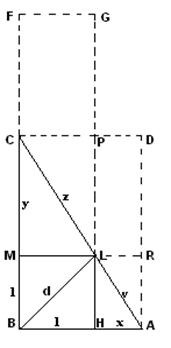 Il
rettangolo costruito sul cateto maggiore, ossia BC, e l'ipotenusa AC
è equivalente al rettangolo costruito sulla somma dei cateti BC+BA
e la parte maggiore dell'ipotenusa che viene divisa dalla bisettrice, ossia
LC. Per cui, indicando con a e b il cateto maggiore e quello
minore, con c l'ipotenusa e con z il segmento maggiore, avremo:
Il
rettangolo costruito sul cateto maggiore, ossia BC, e l'ipotenusa AC
è equivalente al rettangolo costruito sulla somma dei cateti BC+BA
e la parte maggiore dell'ipotenusa che viene divisa dalla bisettrice, ossia
LC. Per cui, indicando con a e b il cateto maggiore e quello
minore, con c l'ipotenusa e con z il segmento maggiore, avremo:
BC AC ~ (BC+BA) LC; da cui:
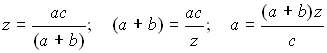
PROBLEMI
Nel triangolo rettangolo ABC, i cateti a e b misurano rispettivamente 28 cm e 21 cm, mentre l'ipotenusa misura 35 cm. Calcolare la misura di z.
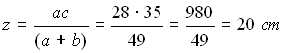
Nel triangolo rettangolo ABC, la somma dei cateti misura 49 cm, l'ipotenusa
misura 35 cm, mentre z misura 20 cm. Calcolare il cateto maggiore.
![]()
Teorema 8

Il rettangolo costruito sul cateto minore BA e il lato del quadrato BM, ossia ABMR, è equivalente al rettangolo costruito sul cateto maggiore BC e la differenza tra il cateto minore e il lato del quadrato AH, ossia AHPD. Perciò avremo:
ABMR = AHPD; da cui:
![]()
Nel triangolo rettangolo ABC, il cateto minore misura 21 cm e x misura 9 cm. Calcolare il cateto maggiore.
![]()
Nel triangolo rettangolo ABC, i cateti misurano 28 cm e 21 cm, mentre il lato
del quadrato inscritto misura 12 cm. Calcolare la misura di x.
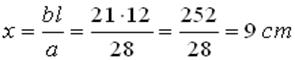
Teorema 9

Il rettangolo costruito sul cateto maggiore BC e il lato del quadrato BH, ossia HBCP, è equivalente al rettangolo costruito sul cateto minore AB e la differenza tra il cateto maggiore BC e il lato del quadrato BM, ossia CDRM. Perciò avremo:
HBCP = CDRM ; da cui:
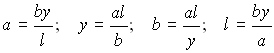
PROBLEMI
Nel triangolo rettangolo ABC, il cateto maggiore misura 28 cm e y misura 16 cm. Calcolare il cateto minore.
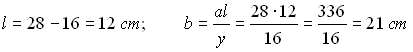
Nel triangolo rettangolo ABC, i cateti misurano 28 cm e 21 cm, mentre il lato del quadrato inscritto misura 12 cm. Calcolare la misura di y.
![]()
2) RISOLuZIONE ALGEBRICA DEL TEOREMA DI PITAGORA
1) In algebra si è studiato il seguente prodotto notevole:
(a-b)2 = a2 + b2 - 2ab; da cui:
2ab + (a-b)2 = a2 + b2
dove:
a e b = cateto maggiore e cateto minore;
2ab= doppio rettangolo costruito sui cateti o doppio prodotto dei cateti;
ab= rettangolo costruito sui cateti o prodotto dei cateti;
(a-b)2 = quadrato della differenza dei cateti;
a2+b2 = quadrato dell'ipotenusa, in quanto somma dei quadrati dei due cateti;
ma dalla seconda uguaglianza sopra riportata, si deduce che il quadrato dell'ipotenusa è dato anche da:
2ab + (a-b)2
Per cui l'ipotenusa è anche uguale al doppio prodotto dei cateti più il quadrato della loro differenza.
Comunque, geometricamente parlando, possiamo dire che il quadrato dell'ipotenusa è equivalente al doppio rettangolo costruito sui cateti più il quadrato costruito sulla differenza degli stessi.
Così, indicando con a, b, c rispettivamente il cateto maggiore, il cateto minore e l'ipotenusa, avremo:
![]()
Ma abbiamo anche:
![]()
Se abbiamo a=12 e b=5, c sarà uguale a:
![]()
![]()
2) In algebra abbiamo ancora il seguente prodotto notevole:
a2-b2 = (a + b) (a b);
dove:
a e b = cateto maggiore e cateto minore;
(a + b) = somma dei cateti;
(a b) = differenza dei cateti;
a2+b2 = quadrato dell'ipotenusa
Per il teorema di Pitagora, il quadrato di un cateto è uguale al quadrato dell'ipotenusa meno il quadrato dell'altro cateto.
Indicando con c l'ipotenusa, abbiamo:
a2 = c2 b2; b2 = c2 a2
Così, indicando con a, b, c rispettivamente il cateto maggiore, il cateto minore e l'ipotenusa e applicando il prodotto notevole sopra riportato, avremo:
a2 = (c + b) (c b);
b2 = (c + a) (c a);
Per cui il quadrato di un cateto è uguale al prodotto tra la somma dell'ipotenusa più l'altro cateto e la loro differenza.
![]()
![]()
In un triangolo rettangolo, se l'ipotenusa misura 25 cm e il
cateto minore misura 7 cm, il cateto maggiore sarà uguale a:
![]()
In un triangolo rettangolo, se l'ipotenusa misura 25 cm e il
cateto maggiore misura 7 cm, il cateto minore sarà uguale a:
![]()
3) TEOREMI GEOMETRICI AL POSTO DI SISTEMI DI EQuAZIONE DI SECONDO GRADO
Nel triangolo rettangolo, alcuni problemi possono essere risolti, ricorrendo a teoremi geometrici ed evitando sistemi di equazione di secondo grado.
Il primo teorema è il seguente:
Il quadrato della somma dei cateti (a+b) più quello della loro differenza (a-b) danno il doppio quadrato dell'ipotenusa 2c .
La sua applicazione si ha nei seguenti tre problemi:
1) In un triangolo rettangolo, l'ipotenusa misura 20 cm e la somma dei cateti misura 28 cm. Calcolare i cateti.
![]()
Sommando poi la somma dei cateti e la loro differenza e dividendo per 2 il risultato, otteniamo il cateto maggiore.
a = (28 + 4) : 2 = 32 : 2 = 16 cm
Sottraendo poi la differenza dei cateti alla loro somma e dividendo per 2 il risultato, otteniamo il cateto minore.
b
= (28 - 4) : 2 = 24 : 2 = 12 cm
2) In un triangolo rettangolo, l'ipotenusa misura 17 cm e la differenza dei cateti misura 7 cm. Calcolare i cateti.
![]()
Sommando poi la somma dei cateti e la loro differenza e dividendo per 2 il risultato, otteniamo il cateto maggiore.
a = (23 + 7) : 2 = 30 : 2 = 15 cm
Sottraendo poi la differenza dei cateti alla loro somma e dividendo per 2 il risultato, otteniamo il cateto minore.
b = (23 - 7) : 2 = 16 : 2 = 8 cm
3) In un triangolo rettangolo, la somma dei cateti misura 31 cm e la differenza dei cateti misura 17 cm. Calcolare l'ipotenusa.
![]()
![]()
Il secondo teorema è il seguente:
Il doppio prodotto dei cateti 2ab più il quadrato della loro differenza (a-b) danno il quadrato dell'ipotenusa.
La sua applicazione si ha nei seguenti tre problemi:
1) In un triangolo rettangolo, l'ipotenusa misura 5 cm e l'area misura 6 cm². Calcolare i due cateti.
![]()
Applicando il teorema 1, avremo la somma dei cateti:
![]()
Conoscendosi la loro somma e la loro differenza, come già visto, i cateti saranno:
a = (7 + 1) : 2 = 8 : 2 = 4 cm ;
b = (7 - 1) : 2 = 6 : 2 = 3 cm
2) In un triangolo rettangolo, l'ipotenusa misura 10 cm, mentre la differenza dei cateti misura 2 cm. Calcolare l'area.
A = (10² - 2²) : 4 = (100 - 4) : 4 = 96 : 4 = 24 cm²
3) In un triangolo rettangolo, l'area misura 30 cm², mentre la differenza dei cateti misura 7 cm. Calcolare l'ipotenusa c.
![]()
4) TEOREMA SuLLE PROIEZIONI DEI CATETI
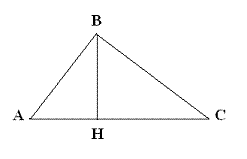
In un triangolo rettangolo, la differenza dei quadrati delle proiezioni dei cateti sull'ipotenusa equivalente al rettangolo che ha per dimensioni la somma e la differenza dei cateti.
CH2 AH2 = (BC + AB) (BC - AB)
Per cui le formule inverse risultano:
BC + AB = (CH2 AH2) : (BC AB)
BC - AB = (CH2 AH2) : (BC + AB)
CH2 = (BC + AB) (BC - AB) + AH2
AH2 = CH2 - (BC + AB) (BC - AB)
PROBLEMI
1) In un triangolo rettangolo, i cateti misurano 40 cm e 30 cm. Calcolare la differenza dei quadrati delle proiezioni dei cateti sull'ipotenusa.
CH2 AH2 = (BC+AB) (BC-AB) = (40+30) (40 30) = 70 10 = 700 cm2
2) In un triangolo rettangolo, le proiezioni dei cateti sull'ipotenusa misura 32 cm e 18 cm, mentre la somma dei cateti misura 70 cm. Calcolare i due cateti.
BC-AB =(CH2 AH2) : (BC+AB)=(322 182) : (40+30)=(1024 324) : 70=700 : 70=10 cm
BC= (70 + 10) : 2 = 80 : 2 = 40 cm
AB = (70 10) : 2 = 60 : 2 = 30 cm
3) In un triangolo rettangolo, le proiezioni dei cateti sull'ipotenusa misura 32 cm e 18 cm, mentre la differenza dei cateti misura 10 cm. Calcolare i due cateti.
BC + AB = (CH2 AH2) : (BC - AB) = (322 182) : (40-30) = (1024 324) : 10 = 700 : 10 = 70 cm
BC= (70 + 10) : 2 = 80 : 2 = 40
AB = (70 10) : 2 = 60 : 2 = 30
4) In un triangolo rettangolo, i cateti misurano 20 cm e 15 cm, mentre la proiezione del cateto minore sull'ipotenusa misura 9 cm. Calcolare la proiezione del cateto maggiore sull'ipotenusa.
CH2=(BC+AB) (BC-AB)+AH2=(20+15)
(20-15) + 92
= 35 5 + 81 = 175+81 = 256, la cui radice quadrata è 16 cm;
5) In un triangolo rettangolo, i cateti misurano 20 cm e 15 cm, mentre la proiezione del
cateto maggiore sull'ipotenusa misura 16 cm. Calcolare la proiezione del cateto
minore sull'ipotenusa.
AH2
= (BC+AB) (BC-AB) (BC+AB)
(BC-AB) + AH2
= (20+15) (20-15) + 92 = 35 5 + 81=175 + 81 = 256; la cui radice quadrata è 16 cm
AH2 = CH2 - (BC+AB) (BC-AB) = 162 - (20+15)(20-15) =
256-35 5 = 256-175 = 81; la cui radice quadrata è 9 cm
Formano una terna pitagorica tre numeri interi, che rappresentano
i lati di un triangolo rettangolo e soddisfano il teorema di Pitagora, nel senso
che la somma dei quadrati dei due più piccoli è equivalente al quadrato del più
grande. Comunque, siccome abbiamo visto che un lato di un triangolo rettangolo,
conoscendo gli altri due, può essere trovato anche senza applicare il teorema di
Pitagora, è improprio chiamarla terna pitagorica, anziché terna di un triangolo
rettangolo.
Gli autori di
testi di Geometria, nei problemi con applicazione del teorema di Pitagora, per
avere risultati interi, ricorrono spesso a tali terne, che per lo più sono
sempre le stesse, come le terne prime: 3, 4 e 5; 5, 12 e 13; 7, 24 e 25; 8, 15 e
17. Da ognuna di esse, si possono poi ricavare infinite terne multiple. Basta
moltiplicare i loro tre numeri per uno stesso numero intero, a cominciare dal 2
fino all'infinito. Per questo ogni terna prima ha una infinità di terne
multiple.
Esempio:
Dalla terna
prima 3, 4 e 5, possiamo avere le terne multiple: 6, 8 e 10; 9, 12 e 15; 12, 16
e 20; 15, 20 e 25; 18, 24 e 30; 21, 28 e 35; 24, 32 e 40; 27, 36 e 45; 30, 40 e
50; 33, 44 e 55; ecc...
Anche le terne
prime di un triangolo rettangolo sono infinite e si possono ricavare facilmente,
applicando le due seguenti regole:
A) Se si parte
da un numero dispari, che viene considerato cateto minore, abbiamo il seguente
procedimento:
Si ricavano
dal cateto minore i due numeri consecutivi, la cui somma dà il cateto stesso.
Dal numero 3 si ricavano 1 e 2; dal numero 5 si ricavano 2 e 3; dal numero 7 si
ricavano 3 e 4. La stessa cosa vale per tutti gli altri numeri dispari
successivi.
Ebbene, il
cateto maggiore è dato dal prodotto di uno dei due numeri ricavati (conviene
sempre raddoppiare il minore) per il doppio dell'altro; mentre l'ipotenusa è
data da tale prodotto più 1.
Nel caso A),
si hanno solo terne primitive.
Così, per
trovare il cateto maggiore e l'ipotenusa, si hanno le due seguenti espressioni
aritmetiche:
Se il cateto
minore è 3 (1+2), abbiamo:
cateto
maggiore: 2 + 2 = 4
ipotenusa: 2 +
2 + 1 = 5
Se il cateto
minore è 5 (2+3), abbiamo:
cateto
maggiore: 4 x 3 = 12
ipotenusa: 4 x
3 + 1 = 13
Se il cateto
minore è 7 (3+4), abbiamo:
cateto
maggiore: 6 x 4 = 24
ipotenusa: 6 x
4 +1 = 25
B) Se si parte
da un numero pari, che viene considerato cateto minore, abbiamo il seguente
procedimento:
Si ricavano
dal cateto minore i due numeri alternati, la cui somma dà il cateto stesso. Dal
numero 4 si ricavano 1 e 3; dal numero 6 si ricavano 2 e 4; dal numero 8 si
ricavano 3 e 5; dal numero 10 si ricavano 4 e 6; dal numero 12 si ricavano 5 e
7. La stessa cosa vale per tutti gli altri numeri dispari successivi.
Ebbene, il
cateto maggiore è dato dal prodotto dei due numeri ricavati; mentre l'ipotenusa
è data da tale prodotto più 2.
Nel caso B),
si hanno sia terne primitive, cioè quelle ottenute da 4 e dai suoi multipli, sia
terne derivate, cioè tutte le altre.
Così, per
trovare il cateto maggiore e l'ipotenusa, si hanno le due seguenti espressioni
aritmetiche:
Se il cateto
minore è 4 (1+3), abbiamo:
cateto
maggiore: 1 x 3 = 3
ipotenusa: 1 x
3 + 2 = 5
(Si tratta
dell'unico caso in cui 4 risulta cateto maggiore, anziché cateto minore, poiché
esso viene a coincidere con la terna ricavata dal numero dispari 3, il quale dà:
3-4-5)
Se il cateto
minore è 6 (2+4), abbiamo:
cateto
maggiore: 2 x 4 = 8
ipotenusa: 2 x
4 + 2 = 10
(terna
multipla di 3-4-5)
Se il cateto
minore è 8 (3+5), abbiamo:
cateto
maggiore: 3 x 5 = 15
ipotenusa: 3 x
5 + 2 = 17
(terna
primitiva)
Se il cateto
minore è 10 (4+6), abbiamo:
cateto
maggiore: 4 x 6 = 24
ipotenusa: 4 x
6 + 2 = 26
(terna
multipla di 5-12-13)
Se il cateto
minore è 12 (5+7), abbiamo:
cateto
maggiore: 5 x 7 = 35
ipotenusa: 5 x
7 + 2 = 37
(terna
primitiva)
Come possiamo
osservare, se i due numeri alternati risultano dispari (solo nei multipli di 4),
essi danno luogo ad una terna primitiva; se invece risultano pari, danno luogo
ad una terna derivata).
C) Se di un
triangolo rettangolo si conoscono i due cateti oppure il cateto minore e
l'ipotenusa, per sapere se essi formano una terna pitagorica, bisogna procedere,
come se stessimo ricavando dal cateto minore quello maggiore o l'ipotenusa. Se
il procedimento ci porta allo stesso cateto maggiore noto o all'ipotenusa nota,
essi formano una terna pitagorica.
Se i cateti
sono 5 e 12, siccome 5 è uguale a 2+3 e il prodotto 4x3 dà 12, i cateti 5 e 12
fanno parte di una terna pitagorica.
Se 5 e 13 sono
rispettivamente il cateto minore e l'ipotenusa, siccome 5 è uguale a 2+3 e il
risultato di 4x3+1 dà 13, 5 e 13 fanno parte di una terna pitagorica.
Se i cateti
sono 8 e 15, siccome 8 è uguale a 3+5 e il prodotto 3x5 dà 15, i cateti 8 e 15
fanno parte di una terna pitagorica.
Se 8 e 15 sono
rispettivamente il cateto minore e l'ipotenusa, siccome 8 à uguale a 3+5 e il
risultato di 3x5+2 dà 17, 8 e 17 fanno parte di una terna pitagorica.
D) Esiste una
certa progressione aritmetica nelle terne primitive, siano esse derivate da
numeri dispari o da numeri pari multipli di 4. La quale è la seguente:
Il cateto
maggiore di una terna primitiva è dato dal cateto minore della terna più la
somma dei cateti della precedente terna.
Esempi:
Se abbiamo la
terna 3, 4 e 5, che è la terna ottenuta con 3, il cateto maggiore della terna di
5 si ottiene, aggiungendo a 5 la somma dei due cateti della terna di 3:
5+7 (3+4) = 12
Per ottenere
l'ipotenusa, si aggiunge sempre una unità al cateto maggiore: 12+1=13.
Se abbiamo la
terna 8, 15 e 17, che è la terna ottenuta con 8, il cateto maggiore della terna
di 12 si ottiene, aggiungendo a 12 la somma dei cateti della terna di 8:
12+23 (8+15) =
35
Per ottenere
l'ipotenusa, si aggiungono sempre due unità al cateto maggiore: 35+2=37.
una
progressione di questo tipo ci permette di ottenere più velocemente le terne
primitive di più numeri in successione, senza ricorrere ogni volta alle due
regole riportate sopra, dopo che si è ottenuta la prima.
(Le terne
pitagoriche in neretto sono primitive)
3-4-5
5-12-13
6-8-10
7-24-25
8-15-17
9-12-15
9-40-41
10-24-26
11-60-61
12-16-20
12-35-37
13-84-85
14-48-50
15-20-25
15-36-39
15-112-113
16-30-34
16-63-65
17-144-145
18-24-30
18-80-82
19-180-181
20-21-29
20-48-52
20-99-101
21-28-35
21-72-75
21-220-221
22-120-122
23-264-265
24-32-40
24-45-51
24-70-74
24-143-145
25-60-65
25-312-313
26-168-170
27-36-45
27-120-123
27-364-365
28-45-53
28-96-100
28-195-197
29-420-421
30-40-50
30-72-78
30-224-226
31-480-481
32-60-68
32-126-130
32-255-257
33-44-55
33-56-65
33-180-183
33-544-545
34-288-290
35-84-91
35-120-125
35-612-613
36-48-60
36-77-85
36-105-111
36-160-164
36-323-325
37-684-685
38-360-362
39-52-65
39-252-255
39-760-761
40-42-58
40-75-85
40-96-104
40-198-202
40-399-401
41-840-841
42-56-70
42-144-150
42-440-442
43-924-925
44-117-125
44-240-244
44-483-485
45-60-75
45-108-117
45-200-205
45-336-339
46-528-530
48-55-73
48-64-80
48-90-102
48-140-148
48-189-195
48-286-290
48-575-577
49-168-175
50-120-130
50-624-626
51-68-85
51-140-149
51-432-435
52-165-173
52-336-340
52-675-677
54-72-90
54-240-246
54-728-730
55-132-143
55-300-305
56-90-106
56-104-119
56-192-200
56-390-394
56-783-785
57-76-95
57-176-185
57-540-543
58-840-842
59-540-549
60-63-87
60-80-100
60-91-109
60-144-156
60-175-185
60-297-303
60-448-452
60-899-901
62-960-962
63-84-105
63-216-225
63-280-287
63-660-663
64-120-126
64-252-260
64-510-514
65-72-97
65-156-169
65-420-429
66-88-110
66-112-130
66-360-366
68-285-293
68-576-580
69-92-115
69-260-269
69-792-795
70-168-182
70-240-250
72-96-120
72-135-153
72-154-170
72-210-222
72-320-328
72-429-435
72-646-650
75-100-125
75-180-195
75-308-317
75-560-565
75-936-939
76-357-365
76-720-724
77-264-275
77-420-427
78-104-130
78-160-178
78-504-510
80-84-116
80-150-170
80-192-208
80-315-325
80-396-404
81-108-135
81-360-369
84-112-140
84-135-159
84-187-205
84-245-259
84-288-300
84-437-445
84-585-591
84-880-884
85-132-157
85-204-221
85-720-725
87-116-145
87-416-425
88-105-137
88-165-187
88-234-250
88-480-488
88-966-970
90-120-150
90-216-234
90-400-410
90-672-678
91-312-325
91-588-595
92-525-533
93-124-155
93-476-485
95-168-193
95-228-247
95-900-905
96-110-146
96-128-160
96-180-204
96-247-265
96-280-296
96-378-390
96-572-580
96-765-771
98-336-350
99-132-165
99-168-195
99-440-451
99-540-549
100-105-145
100-248-260
100-495-505
100-621-629
102-136-170
102-280-298
102-864-870
104-153-185
104-195-221
104-330-346
104-672-680
105-140-175
105-do8-233
105-252-273
105-360-375
105-608-617
105-784-791
108-144-180
108-231-255
108-315-333
108-480-492
108-725-733
110-264-286
110-600-610
111-148-185
111-680-689
112-180-212
112-210-238
112-384-400
112-441-455
112-780-788
114-152-190
114-352-370
115-252-277
115-276-299
116-837-845
117-156-195
117-240-267
117-520-533
117-756-765
119-120-169
119-408-425
120-126-174
120-160-200
120-182-218
120-209-241
120-225-255
120-288-312
120-350-370
120-391-409
120-442-458
120-594-606
120-715-725
120-896-904
121-660-671
123-164-205
123-836-845
124-957-965
125-300-325
126-168-210
126-432-450
126-560-574
128-240-272
128-504-520
129-172-215
129-920-929
130-144-194
130-312-338
130-840-850
132-176-220
132-224-260
132-351-375
132-385-407
132-475-493
132-720-732
133-156-205
133-466-475
135-180-225
135-324-351
135-352-377
135-600-615
136-255-289
136-273-305
136-570-586
138-184-230
138-520-538
140-147-203
140-171-221
140-225-265
140-336-364
140-480-500
140-693-707
140-975-985
141-188-235
143-780-793
143-924-935
144-165-219
144-192-240
144-270-306
144-308-340
144-420-444
144-567-585
144-640-656
144-858-870
145-348-377
145-408-433
147-196-245
147-504-525
150-200-250
150-360-390
150-616-634
152-285-323
152-345-377
152-714-730
153-420-447
153-680-697
154-528-550
154-840-854
155-372-403
155-468-493
156-208-260
156-320-356
156-455-481
156-495-519
156-667-685
159-212-265
160-168-232
160-231-281
160-300-340
160-384-416
160-630-650
160-792-808
161-240-289
161-552-575
162-216-270
162-720-738
165-220-275
165-280-325
165-396-429
165-532-557
165-900-915
168-224-280
168-270-318
168-374-410
168-425-457
168-490-518
168-576-600
168-775-793
168-874-890
170-264-314
170-408-442
171-228-285
171-528-555
171-760-779
174-232-290
174-832-850
175-288-337
175-420-455
175-600-625
176-210-274
176-330-374
176-468-500
176-693-715
176-960-976
177-236-295
180-189-261
180-240-300
180-273-327
180-299-349
180-385-425
180-432-468
180-663-687
180-800-820
180-891-909
182-624-650
183-244-305
184-345-391
184-513-545
185-444-481
185-672-697
186-248-310
186-952-970
189-252-315
189-340-389
189-648-675
189-840-861
190-336-386
190-456-494
192-220.292
192-256-320
192-360-408
192-494-530
192-560-592
192-576-780
195-216-291
195-260-325
195-400-445
195-468-507
195-748-773
196-315-371
196-672-700
198-264-330
198-336-390
198-880-902
200-210-290
200-375-425
200-480-520
200-609-641
201-268-335
203-396-445
203-696-725
204-253-325
204-272-340
204-560-596
204-595-629
204-855-879
205-492-533
205-828-853
207-224-305
207-276-345
207-780-807
207-920-943
208-306-370
208-390-442
208-660-692
208-819-910
210-280-350
210-416-466
210-504-546
210-720-750
213-284-355
215-516-559
215-812-937
216-288-360
216-405-459
216-462-510
216-713-745
216-960-984
217-456-505
217-744-775
219-292-365
220-231-319
220-459-509
220-528-572
220-585-625
222-296-370
224-360-424
224-420-476
224-768-800
224-882-910
225-272-353
225-300-375
225-540-585
225-924-941
228-304-330
228-325-397
228-665-703
228-704-740
230-504-554
230-552-598
231-308-385
231-392-455
231-520-569
231-792-825
232-435-493
232-825-857
234-312-390
234-480-534
235-564-611
236-527-625
237-316-395
238-240-338
238-816-850
240-252-348
240-275-365
240-320-400
240-364-436
240-418-482
240-450-510
240-551-601
240-576-624
240-700-740
240-782-818
240-884-916
243-324-405
245-588-637
245-840-875
246-328-410
248-465-527
248-945-977
249-332-415
250-600-630
252-275-373
252-336-420
252-405-477
252-539-595
252-561-615
252-735-777
252-864-900
255-340-425
255-396-471
255-612-663
255-700-745
256-480-544
258-344-430
259-660-709
259-888-925
260-273-377
260-288-388
260-624-676
260-651-701
260-825-865
261-348-435
261-380-461
264-315-411
264-352-440
264-448-420
264-495-561
264-702-750
264-770-814
264-950-986
265-636-689
266-312-410
266-912-950
267-356-445
270-360-450
270-648-702
270-704-754
272-510-578
272-546-610
273-364-455
273-560-623
273-736-785
273-936-975
275-660-715
276-368-460
276-493-565
276-805-851
279-372-465
279-440-521
280-294-406
280-342-442
280-351-449
280-450-530
280-525-595
280-672-728
280-759-809
280-960-1000
282-376-470
285-380-475
285-504-579
285-684-741
285-880-925
287-716-865
288-330-438
288-384-480
288-540-612
288-616-680
288-741-795
288-840-888
290-696-754
290-816-866
291-388-485
294-392-490
295-708-767
296-555-629
300-315-435
300-400-500
300-455-545
300-589-661
300-720-780
300-875-925
301-900-949
303-404-505
304-570-646
304-650-754
305-732-793
306-408-510
306-840-894
308-435-533
308-495-583
308-819-875
309-412-415
310-744-806
310-936-986
312-416-520
312-459-555
312-585-663
312-640-712
315-420-525
315-572-653
315-624-600
315-756-819
318-424-530
319-360-481
320-336-464
320-462-562
320-600-680
321-428-535
322-480-578
324-432-540
324-693-765
324-945-999
325-360-485
325-780-845
327-436-545
328-615-697
330-440-550
330-560-650
330-792-858
332-495-657
333-444-555
333-644-725
335-804-871
336-377-505
336-385-511
336-448-560
336-540-636
336-630-714
336-748-820
336-850-914
339-452-565
340-528-628
340-357-493
340-816-884
341-420-541
342-456-570
344-645-731
345-460-575
345-756-831
345-828-897
348-464-580
348-805-877
350-576-674
350-840-910
351-468-585
352-420-548
352-660-748
352-936-1000
354-472-590
355-852-923
357-360-507
357-476-595
360-378-522
360-480-600
360-546-654
360-598-698
360-627-723
360-770-850
360-864-936
363-484-605
363-616-715
364-485-689
364-627-725
365-876-949
366-488-610
368-465-593
368-690-782
369-492-615
369-800-881
370-888-962
372-496-620
372-925-997
375-500-625
375-900-975
376-705-799
378-504-630
378-680-778
380-399-551
380-672-772
380-912-988
381-508-635
384-440-584
384-512-640
385-552-673
387-516-645
387-884-945
390-432-582
390-520-650
390-800-890
392-630-742
392-735-833
393-524-655
396-403-565
396-528-660
396-672-780
396-847-935
399-468-615
399-532-665
400-430-580
400-561-689
400-750-850
402-536-670
405-540-675
406-792-890
407-524-745
408-506-650
408-544-680
408-765-867
408-819-915
411-548-685
414-448-610
414-552-690
416-612-740
416-780-884
417-556-695
420-441-609
420-513-663
420-560-700
420-637-763
420-675-795
420-832-932
420-851-949
423-564-705
424-795-901
425-660-785
426-568-710
428-455-697
429-460-629
429-572-715
429-700-821
429-728-865
429-880-918
432-495-657
432-576-720
432-665-793
432-810-918
435-580-725
438-584-730
440-462-638
440-525-685
440-825-935
441-588-735
444-592-740
447-596-745
448-720-848
448-840-952
450-544-706
450-600-750
451-780-901
453-604-755
455-504-679
456-608-760
456-650-794
456-855-969
459-612-755
460-483-667
462-616-770
462-784-910
464-777-905
464-870-986
465-620-775
468-595-757
468-624-780
471-628-785
473-864-985
474-632-790
475-840-965
476-480-676
476-765-901
477-636-795
480-504-696
480-550-730
480-640-800
480-693-843
480-728-872
480-836-864
481-600-769
483-644-805
483-720-867
486-648-810
489-652-815
492-656-820
495-660-825
495-840-975
498-664-830
500-525-725
501-668-835
504-550-746
504-672-840
504-703-865
504-810-954
507-676-845
510-680-850
510-792-956
513-684-855
516-688-860
519-492-865
520-546-754
520-576-776
520-765-925
522-696-870
522-760-922
525-700-875
528-605-803
528-630-822
528-704-880
531-708-885
532-624-820
533-756-925
534-712-890
540-567-783
540-629-829
540-720-900
540-819-981
543-724-905
546-728-910
549-732-915
552-736-920
555-572-797
555-740-925
558-744-930
560-588-812
560-684-884
560-702-898
561-748-935
564-752-940
567-756-945
570-760-950
573-764-955
576-660-876
576-768-960
579-772-965
580-609-841
580-741-941
582-776-970
585-648-873
585-780-975
588-784-980
591-788-985
594-608-950
594-792-990
595-600-845
597-796-995
600-630-870
600-800-1000
612-759-975
615-728-953
616-663-905
616-735-959
620-651-899
621-672-915
624-715-949
640-672-928
650-720-970
660-693-957
680-714-986
696-697-985
12) RADICE DEI QuADRATI COMPRESI ENTRO IL 10.000
Per eseguire
una moltiplicazione diretta bisogna memorizzare il grafico posto sulla sinistra
(il grafico si ottiene, unendo ogni estremo superiore di una linea con gli
estremi inferiori delle altre linee), tenendo presente: 1) ogni linea
rappresenta un prodotto dato dai due fattori posti ai suoi estremi; 2) ogni
pallino centrale indica un prodotto o la somma di due o pi prodotti, a seconda
delle linee che passano per esso; 3) alle somme centrali dei prodotti, come pure
al prodotto finale, va aggiunto l'eventuale riporto.
23
14
=
----------
322
Nella
moltiplicazione 23 × 14, avremo:
4 × 3 =12 (2 si scrive e 1 si riporta); 4 × 2 + 1 × 3 = 11 + 1 (riporto) = 12 (2 si scrive e 1 si riporta); 1 × 2 = 2 + 1 (riporto) = 3 (si scrive 3)
Risultato finale: 322
123
243
=
-------------
29.889
1234
2104 =
---------------
Nella
moltiplicazione 123 × 243, avremo:
3 × 3 = 9 (si scrive 9); 3 × 2 + 4 × 3 = 18 (8 si scrive e 1 si riporta); 3 × 1 + 2 × 3 + 4 × 2 = 17 + 1 (riporto) = 18 (8 si scrive e 1 si riporta); 4 × 1 + 2 × 2 = 8 + 1 (riporto) = 9 (si scrive 9); 2 × 1 = 2 (si scrive 2)
Risultato finale: 29.889
Nella
moltiplicazione 1234 × 2104, avremo:
4 × 4 = 16 (6 si scrive e 1 si riporta); 4 × 3 + 0 × 4 = 12 + 1 (riporto) = 13 (3 si scrive e 1 si riporta); 4 × 2 + 1 × 4 + 0 × 3 = 12 + 1 (riporto) = 13 (3 si scrive e 1 si riporta); 4 × 1 + 2 × 4 + 1 × 3 + 0 × 2 =15 + 1 (riporto) = 16 (6 si scrive e 1 si riporta); 2 × 3 + 0 × 1 + 1 × 2 = 8 + 1 (riporto) = 9 (si scrive 9); 1 × 1 + 2 × 2 = 5 (si scrive 5); 2 × 1 = 2 (si scrive 2)
Risultato finale: 2.596.336
15) MOLTIPLICAZIONI PER 11
Numeri con due cifre
19)Nomi dei Multipli e dei Sottomultipli delle Potenze
del 10 Nome
Valore Suffisso Simbolo viev=unit 100 v ciov=decina (deca) 101 iov cv ziuv=centinaio (hecto) 102 iuv zv vieb=migliaio 103 ieb vb ciob=decamigliaio 104 iob cb ziub=hectomigliaio 105 iub zb vief=milione 106 ief fv ciof=decamilione 107 iof cf ziuf=hectomilione 108 iuf zf viek=miliardo 109 iek vk ciok=decamiliardo 1010 iok ck ziuk=hectomiliardo 1011 iuk zk viel=bilione 1012 iel vl ciol=decabilione 1013 iol cl ziul=hectobilione 1014 iul zl viem=biliardo 1015 iem vm ciom=decabiliardo 1016 iom cm zium=hectobiliardo 1017 ium zm viep=trilione 1018 iep vp ciop=decatrilione 1019 iop cp ziup=hectotrilione 1020 iup zp vier=triliardo 1021 ier vr cior=decatriliardo 1022 ior cr ziur=hectotriliardo 1023 iur zr vies=quadrilione 1024 ies vs cios=decaquadrilione 1025 ios cs zius=hectoquadrilione 1026 ius zs viet=quadriliardo 1027 iet vt ciot=decaquadriliardo 1028 iot ct ziut=hectoquadriliardo 1029 iut zt
5) TERNE PITAGORICHE
6) TERNE PITAGORICHE ENTRO IL 1000
B) ARITMETICA
7) COME OTTENERE I NuMERI PRIMI
I numeri primi si ottengono mediante due passaggi. Con il primo, avremo tutti i numeri primi contenuti in una certa quantità e i loro
multipli ottenuti con i loro quadrati e le loro moltiplicazioni con i numeri primi più grandi. Con il secondo passaggio, ci sarà
l'eliminazione di tali prodotti, la quale ci permetterà di avere soltanto i numeri primi.
PRIMO PASSAGGIO
Tale passaggio, come è stato anticipato, ci farà ottenere, nello stesso tempo, tutti i numeri primi e i loro multipli ottenuti come indicato, senza che li si possano distinguere. Gli uni e gli altri si avranno, eseguendo addizioni continue con gli operatori 4 e 2, avendo come partenza l'unità, ossia 1. Via via vanno anche eliminati i multipli di 5.
Così fino a 97, escluso il numero primo 3, avremo:
1+4=5+2=7+4=11+2=13+4=17+2=19+4=23+2=25+4=29+2=31+4=35+2=37+4=41+2=43+4=47+2=49+4=53+2=55+4=59+2=61+4=65+2=67+4=71+2=73+4=77+2=79+4=83+2=85+4=89+2=91+4=95+2=97.
Invece, da 97 a 200, avremo:
97+4=101+2=103+4=107+2=109+4=113+2=115+4=119+2=121+4=125+2=127+4=131+2=133+4=137+2=139+4=143+2=145+4=149+2=151+4=155+2=157+4=161+2=163+4=167+2=169+4=173+2=175+4=179+2=181+4=185+2=187+4=191+2=193+4=197+2=199.
SECONDO PASSAGGIO
Ottenuti i seguenti numeri, con l'eliminazione dei multipli del 5:
5-7-11-13-17-19-23-29-31-37-41-43-47-49-53-59-61-67-71-73-77-79-83-89-91-97-101-103-107-109-113-119 -121 -127-131-133 -137-139 -143 -149-151-157-161 -163-167-169 -173-179-181-187 -191-193-197-199, si va alla ricerca dei numeri primi.
In tale serie di numeri, una volta eliminati i multipli del 7 (7x7=49, 7x11= 77, 7x13=91, 7x17=119, 7x19=133, 7x23=161), i multipli dell 11 (11x11=121, 11x13=143, 11x17=187), i multipli del 13 (13x13=169), restano solo i numeri primi.
Continuando con tale metodo, si ottiene la seguente prima tabella parziale, dove risultano i numeri primi (con il puntino accanto) e i loro multipli, come fatto presente:
2.
3.
7.
11.
13.
17.
19.
23.
29.
31.
37.
41.
43.
47.
49
53.
59.
61.
67.
71.
73.
77
79.
83.
89.
91
97.
101.
103.
107.
109.
113.
119
121
127.
131.
133
137.
139.
143
149.
151.
157.
161
163.
167.
169
173.
179.
181.
187
191.
193.
197.
199.
203
209
211.
217
221
223.
227.
229.
233.
239.
241.
247
251.
253
257.
259
263.
269.
271.
277.
281.
283.
287
289
293.
299
301
307.
311.
313.
317.
319
323
329
331.
337.
341
343
347.
349.
353.
359.
361
367.
371
373.
377
379.
383.
389.
391
397.
401.
403
407
409.
413
419.
421.
427
431.
433.
437
439.
443.
449.
451
457.
461.
463.
467.
469
473
479.
481
487.
491.
493
497
499.
503.
509.
511
517
521.
523.
527
529
533
539
541.
547.
551
553
557.
559
563.
569.
571.
577.
581
583
587.
589
593.
599.
601.
607.
611
613.
617.
619.
623
629
631.
637
641.
643.
647.
649
653.
659.
661.
667
671
673.
677.
679
683.
701.
703
707
709.
713
719.
721
727.
731
733.
737
739.
743.
749
751.
757.
761.
763
767
769.
773.
779
781
787.
791
793
797.
799
689
691.
697
803
809.
811.
817
821.
823.
827.
829.
833
839.
841
847
851
853.
857.
859.
863.
869
871
877.
881.
883.
887.
889
893
899
901
907.
911.
913
917
919.
923
929.
931
937.
941.
943
947.
949
953.
959
961
967.
971.
973
977.
979
983.
989
991.
997.
1001
1003
1007
1009.
1013.
1019.
1021.
1027
1031.
1033.
1037
1039.
1043
1049.
1051.
1057
1061.
1063.
1067
1069.
1073
1079
1081
1087.
1091.
1093.
1097.
1099
1103.
1109.
1111
1117.
1121
1123.
1127
1129.
1133
1139
1141
1147
1151.
1153.
1157
1159
1163.
1169
1171.
1177
1181.
1183
1187.
1189
1193.
1199
1201.
1207
1211
1213.
1217.
1219
1223.
1229.
1231.
1237.
1241
1243
1247
1249.
1253
1259.
1261
1267
1271
1273
1277.
1279.
1283.
1289.
1291.
1297.
1301.
1303.
1307.
1309
1313
1319.
1321.
1327.
1331
1333
1337
1339
1343
1349
1351
1357
1361.
1363
1367.
1369
1373.
1379
1381.
1387
1391
1393
1397
1399.
1403
1409.
1411
1417
1421
1423.
1427.
1429.
1433.
1439.
1441
1447.
1451.
1453.
1457
1459.
1463
1469
1471.
1477
1481.
1483.
1487.
1489.
1493.
1499.
1501
1507
1511.
1513
1517
1519
1523.
1529
1531.
1537
1541
1543.
1547
1549.
1553.
1559.
1561
1567.
1571.
1573
1577
1579.
1583.
1589
1591
1597.
1601.
1603
1607.
1609.
1613.
1619.
1621.
1627.
1631
1633
1637.
1639
1643
1649
1651
1657.
1661
1663.
1667.
1669.
1673
1679
1681
1687
1691
1693.
1697.
1699.
1703
1709.
1711
1717
1721.
1723.
1727
1729
1733.
1739
1741.
1747.
1751
1753.
1757
1759.
1763
1769
1771
1777.
1781
1783.
1787.
1789.
1793
1799
1801.
1807
1811.
1813
1817
1819
1823.
1829
1831.
1837
1841
1843
1847.
1849
1853
1859
1861.
1867.
1871.
1873.
1877.
1879.
1883
1889.
1891
1897
1901.
1903
1907.
1909
1913.
1919
1921
1927
1931.
1933.
1937
1939
1943
1949.
1951.
1957
1961
1963
1967
1969
1973.
1979.
1981
1987.
1991
1993
1997.
1999.
2003.
2009
2011.
2017.
2021
2023
2027.
2029.
2033
2039.
2041
2047
2051
2053.
2057
2059
2063.
2069.
2071
2077
2081.
2083.
2087.
2089.
2093
2099.
2101
2107
2111.
2113.
2117
2119
2123
2129.
2131.
2137.
2141.
2143.
2147
2149
2153.
2159
2161.
2167
2171
2173
2177
2179.
2183
2189
2191
2197
2201
2203.
2207.
2209
2213.
2219
2221.
2227
2231
2233
2237.
2239.
2243.
2249
2251.
2257
2261
2263
2267.
2269.
2273.
2279
2281.
2287.
2291
2293.
2297.
2299
2303
2309
2311.
2317
2321
2323
2327
2329
2333.
2339.
2341.
2347.
2351.
2353
2357.
2359
2363
2369
2371.
2377.
2381.
2383.
2387
2389.
2393.
2399.
2401
2407
2411.
2413
2417.
2419
2423.
2429
2431
2437.
2441.
2443
2447.
2449
2453
2459.
2461
2467
2471
2473.
2477.
2479
2483
2489
2491
2497
2501
2503.
2507
2509
2513
2519
2521.
2527
2531.
2533
2537
2539.
2543.
2549.
2551.
2557.
2561
2563
2567
2569
2573
2579.
2581
2587
2591.
2593.
2597
2599
2603
2609.
2611
2617.
2621.
2623
2627
2629
2633.
2639
2641
2647.
2651
2653
2657.
2659.
2663.
2669
2671.
2677.
2681
2683.
2687.
2689.
2693.
2699.
2701
2707.
2711.
2713.
2717
2719.
2723
2729.
2731.
2737
2741.
2743
2747
2749.
2753.
2759
2761
2767.
2771
2773
2777.
2779
2783
2789.
2791.
2797.
2801.
2803.
2807
2809
2813
2819.
2821
2827
2831
2833.
2837.
2839
2843.
2849
2851.
2857.
2861.
2863
2867
2869
2873
2879.
2881
2887.
2891
2893
2897.
2899
2903.
2909.
2911
2917.
2921
2923
2927.
2929
2933
2939.
2941
2947
2951
2953.
2957.
2959
2963.
2969.
2971.
2977
2981
2983
2987
2989
2993
2999.
3001.
3007
3011.
3013
3017
3019.
3023.
3029
3031
3037.
3041.
3043
3047
3049.
3053
3059
3061.
3067.
3071
3073
3077
3079.
3083.
3089.
3091
3097
3101
3103
3107
3109.
3113
3119.
3121.
3127
3131
3133
3137.
3139
3143
3149
3151
3157
3161
3163.
3167.
3169.
3173
3179
3181.
3187.
3191.
3193
3197
3199
3203.
3209.
3211
3217.
3221.
3223
3227
3229.
3233
3239
3241
3247
3251.
3253.
3257.
3259.
3263
3269
3271.
3277
3281
3283
3287
3289
3293
3299.
3301.
3307.
3311
3313.
3317
3319.
3323.
3329.
3331.
3337
3341
3343.
3347.
3349
3353
3359.
3361.
3367
3371.
3373.
3377
3379
3383
3389.
3391.
3397
3401
3403
3407.
3409
3413.
3419
3421
3427
3431
3433.
3437
3439
3443
3449.
3451
3457.
3461.
3463.
3467.
3469.
3473
3479
3481
3487
3491.
3493
3497
3499.
3503
3509
3511.
3517.
3521
3523
3527.
3529.
3533.
3539.
3541.
3547.
3551
3553
3557.
3559.
3563
3569
3571.
3577
3581
3583.
3587
3589
3593.
3599
3601
3607.
3611
3613.
3617.
3619
3623.
3629
3631.
3637.
3641
3643.
3647
3649
3653
3659.
3661
3667
3671.
3673.
3677.
3679
3683
3689
3691.
3697.
3701.
3703
3707
3709.
3713
3719.
3721
3727.
3731
3733.
3737
3739.
3743
3749
3751
3757
3761.
3763
3767.
3769.
3773
3779.
3781
3787
3791
3793.
3797.
3799
3803.
3809
3811
3817
3821.
3823.
3827
3829
3833.
3839
3841
3847.
3851.
3853.
3857
3859
3863.
3869
3871
3877.
3881.
3883
3887
3889.
3893
3899
3901
3907.
3911.
3913
3917.
3919.
3923.
3929.
3931.
3937
3941
3943.
3947.
3949
3953
3959
3961
3967.
3971
3973
3977
3979
3983
3989.
3991
3997
4001.
4003.
4007.
4009
4013.
4019.
4021.
4027.
4031
4033
4037
4039
4043
4049.
4051.
4057.
4061
4063
4067
4069
4073.
4079.
4081
4087
4091.
4093.
4097
4099.
4103
4109
4111.
4117
4121
4123
4127.
4129.
4133.
4139.
4141
4147
4151
4153.
4157.
4159.
4163
4169
4171
4177.
4181
4183
4187
4189
4193
4199
4201
4207
4211
4213
4217.
4219.
4223
4229.
4231.
4237
4241.
4243.
4247
4249
4253.
4259.
4261
4267
4271.
4273.
4277
4279
4283.
4289.
4291
4297.
4301
4303
4307
4309
4313
4319
4321
4327.
4331
4333
4337.
4339.
4343
4349.
4351
4357.
4361
4363.
4367
4369
4373.
4379
4381
4387
4391.
4393
4397.
4399
4403
4409.
4411
4417
4421.
4423.
4427
4429
4433
4439
4441.
4447.
4451.
4453
4457.
4459
4463.
4469
4471
4477
4481.
4483.
4487
4489
4493.
4499
4501
4507.
4511
4513.
4517.
4519.
4523.
4529
4531
4537
4541
4543
4547.
4549.
4553
4559
4561.
4567.
4571
4573
4577
4579
4583.
4589
4591.
4597.
4601
4603.
4607
4609
4613
4619
4621.
4627
4631
4633
4637.
4639.
4643.
4649.
4651.
4657.
4661
4663.
4667
4669
4673.
4679.
4681
4687
4691.
4693
4697
4699
4703.
4709
4711
4717
4721.
4723.
4727
4729.
4733.
4739
4741
4747
4751.
4753
4757
4759.
4763
4769
4771
4777
4781
4783.
4787.
4789.
4793.
4799.
8) DAI MuLTIPLI DEL 6 AI NuMERI PRIMI
a) un numero primo risulta sempre un multiplo di 6, a cui è stata aggiunta o sottratta l'unità. Esso può (ma non obbligatoriamente) derivare dalla sottrazione o dall'aggiunta dell'unità, oppure da entrambe le operazioni. In quest'ultimo caso, i due numeri primi ottenuti sono detti gemelli. Ne deriva che un numero dispari, che non termina con 5, può essere primo, se risulta un multiplo di 6, dopo aver aggiunto o sottratto ad esso l unità, oppure in entrambi i casi.
Ad esempio, se prendiamo 24, che è un multiplo di 6, esso ci dà un numero primo, solo se sottraiamo ad esso l'unità, ottenendo 23. Se invece aggiungiamo ad esso l' unità, otteniamo il numero composto 25.
Se invece prendiamo 18, che è anche un multiplo di 6, aggiungendo e sottraendo ad esso l'unità, otteniamo rispettivamente i due numeri primi 17 e 19, che sono detti gemelli. Infatti, due numeri primi aventi per differenza 2 prendono il nome di gemelli.
I multipli del 6, nei loro rapporti con i numeri primi, risultano di quattro tipi:
1) Multipli che non danno alcun numero primo, sia che si aggiunga ad essi l'unità sia che si sottragga dagli stessi l'unità:
120-1=119; 120+1=121. (119 e 121 non sono numeri primi).
2) Multipli che danno un numero primo, solo se si aggiunge ad essi l'unità:
36+1=37 (37 è numero primo).
3) Multipli che danno un numero primo, solo se si sottrae ad essi l'unità:
54-1=53 (53 è numero primo).
4) Multipli che danno un numero primo, sia che si aggiunga sia che si sottragga ad essi l'unità:
132+1=133; 132-1=131 (133 e 131 sono numeri primi)
Ci sono pure tre tipi di coppie di numeri primi gemelli:
1) Coppia, nella quale il numero primo minore termina con 1 e il maggiore termina con 3, come le seguenti:
11-13; 41-43; 71-73; 101-103; 191-193; 281-283.
2) Coppia, nella quale il numero primo minore termina con 7 e il maggiore termina con 9, come le seguenti:
17-19; 107-109; 137-139; 197-199; 227-229; 347-349.
3) Coppia, nella quale il numero primo minore termina con 9 e il minore termina con 1, come le seguenti:
29-31; 59-61; 149-151; 239-241; 269-271; 599-601.
Risulta divisibile per 6 anche la somma di due numeri primi ottenuti l'uno con +1 e l'altro con -1.
73 (72+1) + 107 (108-1) = 180 (divisibile per 6).
Se due numeri primi sono stati ottenuti entrambi con +1, sottraendo alla loro somma due unità, si ottiene un numero divisibile per 6.
151 (150+1) + 277 (276+1) = 428 - 2 = 426 (divisibile per 6).
Se due numeri primi sono stati ottenuti entrambi con -1, aggiungendo alla loro somma due unità, si ottiene un numero divisibile per 6.
269 (270-1) + 605 (606-1) = 874 + 2 = 876 (divisibile per 6)
b) Se un quadrato è divisibile solo per se stesso e per la sua radice, quest'ultima è un numero primo.
49 è divisibile solo per se stesso e per 7, che è la sua radice. Per cui 7 è un numero primo.
Allora è vero anche che il quadrato di un numero primo è il suo primo multiplo avente come fattori la sua radice.
Il quadrato di 7 è 49, i cui fattori sono 7x7.
c) Se dividiamo un numero primo per 6, avremo come resto 1 oppure 5, a seconda se è stata aggiunta oppure tolta l'unità.
31 : 6 = 5 col resto di 1 (Infatti al multiplo 30 è stata sommata l'unità, facendolo diventare 31, che è un numero primo).
29 : 6 = 4 col resto di 5 (Infatti, al multiplo 30 è stata sottratta l'unità, facendolo diventare 29, che è un numero primo).
d) un numero primo è anche la somma di un multiplo di 6 più un numero primo più piccolo di quello che si vuole ottenere. Quando il multiplo di 6 termina con 0, ad esso non si può sommare il numero primo 5, poiché ne verrebbe fuori un multiplo di 5. A volte lo stesso multiplo di 6, con i vari numeri primi aggiunti, dà luogo ad altrettanti numeri primi. Come pure due addendi diversi, sommati, possono dare lo stesso numero primo.
6 + 11 = 17 (11 e 17 sono numeri primi);
12 + 5 = 17 (5 e 17 sono numeri primi);
6 + 23 = 29 (23 e 29 sono numeri primi);
12 + 19 = 31 (19 e 31 sono numeri primi);
18 + 19 = 37 (19 e 37 sono numeri primi);
42 + 59 = 101 (59 e 101 sono numeri primi); ecc
e) Se si vuole sapere quale multiplo di 6 ha dato origine al numero primo, bisogna prima renderlo multiplo di 6 (aggiungendo o sottraendo ad esso l'unità), come di seguito:
Se abbiamo il numero primo 56443 e vogliamo conoscere il multiplo di 6 che gli ha dato origine, prima eseguiamo le due operazioni e sommiamo le cifre dei due risultati [56443+1=56444 (23)], [56443-1=56442 (21)]. Essendo 21 divisibile per 3, 56442 risulta divisibile per 6. Per cui il multiplo di 6 che ha dato origine al numero primo 56443 è 56442.
Nel caso di due numeri primi gemelli, come 34757 e 34759, il multiplo di 6, che ha dato origine ad entrambi, è il loro numero intermedio, ossia 34758.
Se la somma di due numeri primi è divisibile per 6, l'uno è stato ottenuto da un multiplo di 6 a cui è stata tolta l'unità e l'altro è stato ottenuto da un multiplo di 6 a cui è stata aggiunta l'unità, come nei seguenti:
317 + 643 = 960 : 6 = 160 (318-1 = 317 / 642+1 = 643)
Nei numeri primi gemelli avviene la stessa cosa. Essi però sono stati ottenuti dallo stesso multiplo di 6.
f) Ogni numero primo ha infiniti multipli, i quali si possono dividere in due gruppi: a) quelli ottenuti dal suo prodotto con numeri non primi, come 9, 10, 12, che sono infiniti; b) quelli ottenuti dal suo prodotto con numeri primi, come 11, 13, 17, che sono pure infiniti. Questo secondo gruppo d origine a dei prodotti aventi per fattori due numeri primi. Cos 91, che un multiplo di 7, ha per fattori 7 e 13. un multiplo di questo tipo possiamo considerarlo multiplo bifattoriale primo; invece 12, che un multiplo di 3 ed ha per fattori 3 e 4, da considerarsi un multiplo bifattoriale non primo. Se nel primo caso il multiplo 91 pu avere una sola coppia di fattori, cio 7 e 13; nel secondo caso, il multiplo 12 pu avere due coppie di fattori, ossia 3 e 4, 2 e 6.
h) I numeri primi terminano sempre con le cifre 1, 3, 7 e 9. Ora vediamo come si ottengono i numeri primi terminanti con tali cifre.
1)I multipli del 6 ottenuti con i numeri terminanti con 2 e con 7 possono diventare numeri primi, sottraendo ad essi una unità. Tali numeri primi terminano tutti con la cifra 1. Esempi:
6 x 32 = 192 1 = 191; 6 x 47 = 282 1 = 281 (191 e 281 sono numeri primi).
Anche i multipli del 6 ottenuti con un multiplo del 5 e aumentati di una unità danno luogo a numeri primi terminanti con 1. Esempi:
6 x 5 = 30 + 1 = 31 / 6 x 30 = 180 + 1 = 181 (31 e 181 sono numeri primi)
Comunque, per avere i numeri primi in ordine crescente, bisogna procedere alternativamente prima con il 2, poi con il 5 e infine con il 7.
2 x 6 = 12 1 = 11 / 5 x 6 = 30 + 1 = 31 / 7x6=42-1=41 (Infatti, i numeri 11, 31 e 41 sono tre numeri primi in ordine crescente).
2) I multipli del 6 ottenuti con i numeri terminanti con 4 e con 9 possono diventare numeri primi, sottraendo ad essi l unità. I numeri primi ottenuti con tale criterio terminano tutti con la cifra 3. Esempi:
6 x 14 = 84 1 = 83 / 6 x 29 = 174 1 = 173
Anche i multipli del 6 ottenuti con i numeri terminanti con 2 e con 7 possono diventare numeri primi, aggiungendo ad essi l'unità. Anche essi terminano tutti con la cifra 3. Esempi:
12 x 6 = 72 + 1 = 73 / 17 x 6 = 102 + 1 = 103 (73 e 103 sono numeri primi)
3) I multipli del 6 ottenuti con i numeri terminanti con 1 e con 6 possono diventare numeri primi, aggiungendo ad essi l'unità. Tali numeri primi terminano con la cifra 7. Esempi:
6 x 6 = 36 + 1 = 37 / 6 x 11 = 66 + 1 = 67 (37 e 67 sono numeri primi)
Anche i multipli del 6 ottenuti con numeri terminanti con 3 e con 8 possono diventare numeri primi, sottraendo ad essi l'unità. Anche essi terminano con la cifra 7. Esempi:
6 x 23 = 138 1 = 137; 6 x 58 = 348 1=347 (Anche i numeri primi ottenuti con tale criterio terminano tutti con la cifra 7)
4) I multipli del 6 ottenuti con i numeri terminanti con 3 e con 8 possono diventare numeri primi, aggiungendo ad essi l'unità. I numeri primi ottenuti con tale criterio terminano tutti con la cifra 9. Esempi:
6 x 13 = 78 + 1 = 79 / 6 x 38 = 228 + 1 = 229 (79 e 229 sono numeri primi)
Anche i multipli del 6 ottenuti con i multipli del 5, diminuiti di una unità, possono diventare numeri primi. Anche essi terminano tutti con la cifra 9. Esempi:
5 x 6 = 30 1 = 29; 30 x 6 = 180 1 = 179 (29 e 179 sono numeri primi)
9) SuI QuADRATI DEI NuMERI INTERI
Esiste una correlazione tra i quadrati in successione e i numeri dispari, la quale è la seguente: partendo da 0, tutti i quadrati successivi si ottengono, aggiungendo ad esso i vari numeri dispari in successione.
Il quadrato di un numero n è uguale alla somma dei primi n numeri dispari. Ossia:
3² = 1+3+5=9;
5² = 1+3+5+7+9=25;
9² = 1+3+5+7+9+11+13+15+17=81.
Se bisogna trovare i quadrati di più numeri consecutivi, basta aggiungere ogni volta al quadrato precedente la loro somma, come qui appresso.
Volendo trovare i quadrati dei numeri da 1 a 10, abbiamo:
1² = 1;
2² =1 + 3 (2 + 1) = 4;
3² = 4 + 5 (2 + 3) = 9;
4² = 9 + 7 (3 + 4) = 16;
5² = 16 + 9 (4 + 5) = 25; ecc.
- Conoscendosi n e il suo quadrato, è semplice conoscere qual è stato il numero dispari più grande della serie di numeri dispari, la cui somma ha dato luogo al quadrato. Infatti, esso si ottiene, moltiplicando n per 2 e sottraendo al prodotto 1.
Se sappiamo che il quadrato di 40 è 1600, sappiamo anche che è stata la somma dei primi 40 numeri dispari a dar luogo a 1600, il più grande dei quali è stato: 40 x 2 - 1 = 79. Per cui, se volessimo trovare il quadrato di 41, basterebbe aggiungere a 1600 il successivo numero dispari, che è 81, (1600 + 81 = 1681). Se invece volessimo trovare il quadrato di 39, basterebbe sottrarre da 1600 il numero dispari più grande, che è 79, (1600 - 79 = 1521).
- Da ciò possiamo dedurre che, tutte le volte che dobbiamo trovare il quadrato dei numeri come 51 e 49, ci conviene trovare prima il quadrato di 50 (2500). Dopo aggiungiamo 101 (2601) per trovare il quadrato di 51 o sottraiamo 99 (2401) per trovare il quadrato di 49.
- Se vogliamo trovare i quadrati di tutti i numeri dispari, a partire dal quadrato 1, basta aggiungere ad esso di seguito 8 e i suoi multipli, come appresso:
1² + 8 = 9 (quadrato di 3) + 16 = 25 (quadrato di 5) + 24 = 49 (quadrato di 7) + 32 = 81 (quadrato di 9) + 40 = 121 (quadrato di 11) + 48 = 169 (quadrato di 13); ecc.
- Se vogliamo trovare i quadrati di tutti i numeri pari, a partire dal quadrato di 2, ossia 4, basta aggiungere ad esso di seguito 8 e i suoi multipli aumentati di 4, come appresso:
4 (quadrato di 2) + 12 (8 + 4) = 16 (quadrato di 4) + 20 (16 + 4) = 36 (quadrato di 6) + 28 (24 + 4) = 64 (quadrato di 8) + 36 (32 + 4) = 100 (quadrato di 10) + 44 (40 + 4) = 144 (quadrato di 12) + 52 (48 + 4) = 196 (quadrato di 14); ecc.
b) Esiste anche una formula per trovare il quadrato di un numero di due cifre, alla quale, senza eseguire la moltiplicazione, possiamo ricorrere, tutte le volte che troviamo la convenienza.
Se a e b sono rispettivamente le decine e le unità del numero, abbiamo la seguente formula aritmetica:
n² = a² + 2ab + b²
Così, dovendo trovare il quadrato di 56, applicando la formula, avremo:
56² =(50² = 2500) + (50 x 6 x 2 = 600) + (6² = 36) = 2500 + 600 + 36 = 3136
Esiste anche una formula per trovare il quadrato di un numero di tre cifre, alla quale, senza eseguire la moltiplicazione, possiamo ricorrere, tutte le volte che troviamo la convenienza.
Se a, b e c sono rispettivamente le centinaia, le decine e le unità del numero, abbiamo la seguente formula aritmetica:
n² = (a²) + (2ab) + (2ac) + (b²) + (2bc) + c²
Così, dovendo trovare il quadrato di 125, applicando la formula, avremo:
125² = (100² = 10000) + (100 x 20 x 2 = 4000); + (100 x 5 x 2 = 1000) + (20² = 400) + (20 x 5 x 2 = 200) + (5² = 25) = 10.000 + 4000 + 1000 + 400 + 200 + 25 = 15.625
c) Se si conoscono il prodotto di due numeri ab (a il maggiore e b il minore), i loro quadrati a² e b², la loro differenza (a-b) oppure la loro somma (a+b), si hanno come formule:
- la loro somma è data dalla differenza dei loro quadrati diviso la loro differenza: a + b = (a² - b²) : (a-b);
- la loro differenza è data dalla differenza dei loro quadrati diviso la loro somma: a - b = (a² - b²) : (a + b);
- il numero maggiore à dato dalla differenza tra il suo quadrato e il loro prodotto diviso la loro differenza: a = a² - ab : (a - b);
- il numero minore è dato dalla differenza tra il loro prodotto e il suo quadrato diviso la loro differenza: b = ab - b² : (a - b).
In pratica, avremo:
Se il prodotto dei due numeri consecutivi a e b è 12 e i loro rispettivi quadrati sono 16 e 9, nonché si conosce la loro differenza 1 oppure la loro somma 7, applicando le formule, avremo:
a + b = (a² - b²) : (a - b) = (16 - 9) : 1 = 7 : 1 = 7;
a b = (a² - b²) : (a - b) = (16 - 9) : 7 = 7 : 7 = 1;
a = a² - ab : (a - b) = 16 - 12 = 4;
b = ab - b² : (a - b) = (12 - 9) : 1 = 3 : 1 = 3
Inoltre, il prodotto dei due numeri è medio proporzionale tra i due quadrati: a² : ab = ab : b².
Perciò avremo:16 : 12 = 12 : 9.
Se la differenza fra due numeri consecutivi è sempre 1, la differenza fra i loro quadrati è la loro somma. Prendendo ad esempio la coppia di numeri 6 e 5, la loro differenza è 1 (6 - 5 = 1); mentre la differenza dei loro quadrati è 11 (6 + 5 = 11). Infatti, 36 - 25 = 11.
10) SuI CuBI DEI NuMERI INTERI
Anche i cubi dei numeri, come i quadrati, sono dati dalla somma di più numeri dispari, ma in modo diverso. Infatti, ciascuno si ottiene come segue:
1) Procedimento con i numeri interi dispari
Volendo conoscere il cubo di 3, esso è dato da tre numeri dispari consecutivi, che si ottengono nel modo seguente: il primo è il quadrato di 3, ossia 9; gli altri due sono 7 (il precedente) e 11, (il successivo). Perciò avremo: 3³=7+9+11=27.
Volendo conoscere il cubo di 5, esso è dato da cinque numeri dispari consecutivi, che si ottengono nel modo seguente: il primo è il quadrato di 5, ossia 25; gli altri quattro sono 21 e 23 (i precedenti), nonché 27 e 29 (i successivi). Perciò avremo: 5³=21+23+25+27+29=125.
1) Procedimento con i numeri interi pari
Volendo conoscere il cubo di 2, esso è dato da due numeri dispari consecutivi, che si ottengono nel modo seguente: il primo è il precedente del quadrato di 2 (che è 4), ossia 3; il secondo è il successivo del quadrato di 2, che è 5. Perciò avremo: 2³=3+5=8
Volendo conoscere il cubo di 4, esso è dato da quattro numeri dispari consecutivi, che si ottengono nel modo seguente: i primi due sono i precedenti del quadrato di 4 (che è 16), ossia 13 e 15; mente gli altri due sono i successivi del quadrato di 4, ossia 17 e 19. Perciò avremo: 4³=13+15+17+19=64
11) IL MEDIANO E I SuOI SIMMETRICI
Dato un numero n, che chiameremo mediano, le coppie di numeri formati con l'aggiunta e la sottrazione di 1, oppure di 2, ecc. sono detti suoi simmetrici. Perciò i simmetrici di 7 sono 7 + 1 = 8 e 7 &ndsh; 1 = 6. Dei due simmetrici, il primo è detto maggiore e il secondo è detto minore. Le coppie di simmetrici di un mediano non sono illimitate, poiché il loro numero è uguale al mediano diminuito di una unità. Ossia, se il mediano è 15, le coppie di simmetrici ad esso appartenenti sono in tutto 14, ossia 14 e 16, 13 e 17, 12 e 18, 11 e 19, ecc.
Adesso possiamo dire che il quadrato di un mediano è dato anche dalla somma del prodotto dei suoi simmetrici più il quadrato della loro semidifferenza. Perciò avremo:
42 = 5 3 + 12 = 15 + 1 = 16 (Qui i simmetrici sono stati ottenuti con +1 e -1)
72= 9 5 + 22 = 45 + 4 = 49 (Qui i simmetrici sono stati ottenuti con +2 e -2)
Se si conoscono due numeri simmetrici, il loro mediano uguale alla loro semisomma. Perciò, se abbiamo i simmetrici 10 e 8, il loro mediano è:
(10 + 8) : 2 = 18 : 2 = 9
In geometria, se il mediano rappresenta il lato di un quadrato, i suoi simmetrici rappresentano le dimensioni di un rettangolo. In tal caso, diciamo che il quadrato e il rettangolo sono in relazione fra loro. Per cui, se un quadrato e un rettangolo sono in relazione fra loro, il lato del quadrato va considerato mediano e le dimensioni del rettangolo vanno considerate suoi simmetrici. La qual cosa può facilitarci la soluzione di alcuni problemi geometrici.
un quadrato e un rettangolo, che ha per dimesioni cm 7 e cm 9, sono in relazione fra loro. Trovare l'area del quadrato.
Essendo 7 e 9 simmetrici, il loro mediano è il lato del quadrato. Perciò:
(7 + 9) : 2 = 16 : 2 = cm 8; da cui:
A = 82 = cm2 64
un rettangolo e un quadrato, che ha per lato cm 13, sono in relazione fra loro. Trovare l'area del rettangolo, la cui dimensione minore misura cm 11.
Se 13 è il mediano e 11 è il simmetrico minore, la dimensione maggiore del rettangolo è cm 15. Allora l'area del rettangolo sarà uguale a:
A = 15 x 11 = cm2 165
Per trovare la radice dei quadrati compresi entro il 10.000, si segue il procedimento sotto riportato. Ma prima occorre sapere che, se il quadrato termina con 1, come unità della radice si avrà 1 o 9, se il quadrato termina con 4, come unità della radice si avrà 2 o 8; se il quadrato termina con 6, come unità della radice si avrà 4 o 6; se il quadrato termina con 5, come unità della radice si avrà 5. Ma ora passiamo a conoscere il procedimento.
1) si staccano nel quadrato due cifre, da destra verso sinistra, come appresso: 256 diventa 2'56; 1156 diventa 11'56.
2) si vede qual è il quadrato più grande che è contenuto nella parte sinistra, nel nostro caso in 2 e in 11. Così conosceremo anche le decine della radice dei quadrati in questione. Come possiamo renderci conto, 1 è il quadrato più grande che è contenuto nel 2, per cui la sua radice è 1; mentre 9 è il quadrato più grande che è contenuto nell'11, per cui la sua radice è 3.
3) siccome 256 termina con 6, come unità della radice si avrà 4 o 6. Allora bisognerà moltiplicare la radice delle decine (1) per il suo successivo (2). Se il prodotto è contenuto nella prima parte del quadrato (2), si avrà 6; se invece non è contenuto, si avrà 4. Nel nostro caso, il 2 (1·2) è contenuto nel 2, per cui la radice delle unità sarà 6. Quindi, avremo che la radice quadrata di 256 è 16.
Se consideriamo 1156, terminando esso con 6, come unità della radice si avrà 4 o 6. Moltiplicando la radice delle decine (3) per il suo successivo (4), avremo come prodotto 12. Siccome esso non è contenuto nell'11, la radice delle unità sarà 4. Quindi, avremo che la radice quadrata di 1156 è 34.
Altri esempi:
Se il quadrato è 121 (1'21), la radice delle decine (1) è 1. Terminando esso con 1, la radice delle unità è 1 o 9. Siccome il 2 (1x2) non è contenuto nell'1, la radice delle unità è 1. Quindi la radice quadrata di 121 è 11.
Se il quadrato è 361 (3'61), la radice delle decine (3) è 1. Terminando esso con 1, la radice delle unità è 1 o 9. Siccome 2 (1·2) è contenuto nel 3, la radice delle unità è 9. Quindi, la radice quadrata di 361 è 19.
Se il quadrato è 324 (3'24), la radice delle decine (3) è 1. Terminando esso con 4, la radice delle unità è 2 o 8. Siccome il 2 (1·2) è contenuto nell'3, la radice delle unità è 8. Quindi la radice quadrata di 324 è 18.
Se il quadrato è 144 (1'44), la radice delle decine (1) è 1. Terminando esso con 4, la radice delle unità è 2 o 8. Siccome 2 (1·2) non è contenuto nell'1, la radice delle unità è 2. Quindi, la radice quadrata di 144 è 12.
Se il quadrato è 625 (6'25), la radice delle decine (6) è 2. Terminando esso con 5, la radice delle unità può essere solo 5. Quindi, la radice quadrata di 625 è 25.
13) RADICE DEI CuBI COMPRESI ENTRO IL 1000.000
Per trovare la radice dei cubi compresi entro il 1000.000, si segue il procedimento sotto riportato. Ma prima occorre sapere che:
a) 1 è il cubo di 1, 8 è il cubo di 2, 27 è il cubo di 3, 64 è il cubo di 4, 125 è il cubo di 5, 216 è il cubo di 6, 343 è il cubo di 7, 512 è il cubo di 8, 729 è il cubo di 9;
b) se il cubo termina con 1, 9, 4, 6 e 5, tali cifre resteranno anche nelle unità delle rispettive radici; se il cubo termina con 2, 8, 3 e 7, le unità delle rispettive radici saranno i loro complementari. Ossia: se il cubo termina con 2, la radice delle unità sarà 8; se invece termina con 8, la radice delle unità sarà 2. Se il cubo termina con 3, la radice delle unità sarà 7, se invece termina con 7, la radice delle unità sarà 3.
Ma ora passiamo a conoscere il procedimento, prendendo come esempi i cubi 19683 e 79507.
1) Si staccano nel cubo tre cifre, da destra verso sinistra, per cui i numeri diventano 19'683 e 79'507.
2) Si vede quali sono i due cubi più grandi che sono contenuti nella loro parte sinistra, che nel nostro caso sono 19 e 79. Come possiamo renderci conto, 8 è il cubo più grande che è contenuto nel 19, per cui la radice delle sue decine è 2; mentre 64 è il cubo più grande che è contenuto in 79, per cui la radice delle sue decine è 4.
3) Per conoscere le due radici delle unità, basta ricordarsi che, se il cubo termina con 1, 9, 4, 6 e 5, tali cifre resteranno anche nelle unità delle rispettive radici; se il cubo termina con 2, 8, 3 e 7, le unità delle rispettive radici saranno i loro complementari. Ossia: se il cubo termina con 2, la radice delle unità sarà 8; se invece termina con 8, la radice delle unità sarà 2. Se il cubo termina con 3, la radice delle unità sarà 7, se invece termina con 7, la radice delle unità sarà 3.
Per cui, prendendo in considerazione i cubi 19683 e 79507, nel primo, la radice delle decine è 2, poiché il suo cubo 8 sta nel 19, e quella delle unità è 7, poiché è il complementare di 3. Così il 2 e il 7 ci danno la radice cubica di 19683, che è 27. Nel secondo cubo, la radice delle decine è 4, poiché il suo cubo 64 sta nel 79, e quella delle unità è 3, poiché è il complementare di 7. Così il 4 e il 3 ci danno la radice cubica di 79507, che è 43.
14) MOLTIPLICAZIONI DIRETTE MEDIANTE IL GRAFICO
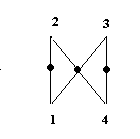
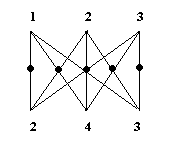
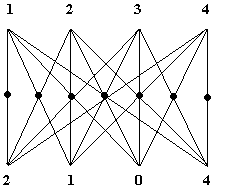
2.596.336
Il prodotto di un numero di due cifre per 11 si ottiene in questo modo: a destra si pone la cifra delle unit del numero e a sinistra si pone il numero stesso aumentato della cifra indicante le sue decine.
Se dobbiamo moltiplicare 36x11, scriviamo a destra 6 e a sinistra 39 (36+3). Quindi il risultato finale sar 396.
Se dobbiamo moltiplicare 17x11, scriviamo a destra 7 e a sinistra 18 (17+1). Quindi il risultato finale sar 187.
Se dobbiamo moltiplicare 36x11, scriviamo a destra 6 e a sinistra 39 (36+3). Quindi il risultato finale sar 396.
Se dobbiamo moltiplicare 92x11, scriviamo a destra 2 e a sinistra 101 (92+9). Quindi il risultato finale sar 1012.
Numeri con tre cifre
Il prodotto di un numero di tre cifre per 11 si ottiene in questo modo: a destra si pone la cifra delle unit del numero e a sinistra si pone il numero stesso aumentato del numero formato dalle sue due prime cifre.
Se dobbiamo moltiplicare 123x11, scriviamo a destra 3 e a sinistra 135 (123+13). Quindi il risultato finale sar 1353.
Se dobbiamo moltiplicare 925x11, scriviamo a destra 5 e a sinistra 1017 (925+92). Quindi il risultato finale sar 10175.
Allo stesso modo si pu procedere anche con numeri che hanno pi di tre cifre.
16) NuOVO SISTEMA NuMERICO IN LETTERE
Prima di andare avanti nell'apprendimento del nuovo sistema numerico in lettere, utile venire a conoscenza della pronuncia delle consonanti usate per formare i numeri. Al riguardo, va fatto presente:
Le vocali E ed O hanno sempre suono aperto, come in setta e in posta;
Le consonanti C e G hanno suono dolce anche davanti ad A, O e u. Il loro suono duro dato rispettivamente dalle consonanti K e H. Perci ha si legge ga e he si legge ghe.
La consonante X ha il suono del sc dolce italiano. Quindi, xa si legge sci e xe si legge sce.
Le consonanti B, D, F, L, M, N, P, R, S, T, V, Z si leggono come nella lingua italiana.
17) I Numeri: dalle unit ai Miliardi
In lettere, i numeri da 0 a 9 sono i seguenti:
Voev=zero; bir=uno; fic=due; kid=tre; lig=quattro; mih=cinque; pin=sei; riv=sette; six=otto; tiz=nove.
I restanti numeri, sempre in lettere, si formano mediante le seguenti regole:
1) Le decine si ottengono, frapponendo una a tra la consonante iniziale e la vocale i delle unit . L accento cade sulla vocale a.
bair=dieci; faic=venti; kaid=trenta; laig=quaranta; maih=cinquanta;
pain=sessanta; raiv=settanta; saix=ottanta; taiz=novanta.
2) Le centinaia si ottengono, frapponendo una e fra la vocale i e la consonante finale delle unit . L accento cade sulla vocale i.
bier=cento; fiec=duecento; kied=trecento; lieg=quattrocento;
mieh=cinquecento; pien=seicento; riev=settecento;
siex=ottocento; tiez=novecento.
3) I numeri formati da decine e unit si ottengono, aggiungendo le unit alle decine e privando queste ultime della loro consonante finale.
Baitiz=diciannove; laimih=quarantacinque; paisix=sessantotto; taibir=novantuno; fairiv=ventisette; maipin=sessantasei; kaific=trentadue; rairiv=settantasette.
4) I numeri formati da centinaia e unit si ottengono, aggiungendo le unit alle centinaia e privando queste ultime della loro consonante finale.
Biebir=centouno; fiekid=duecentotre; lietiz=quattrocentonove; miesix=cinquecentootto; piemih=seicentocinque; rielig=settecentoquattro; kiekid=trecentotre.
5) I numeri formati da centinaia e decine si ottengono, aggiungendo le decine alle centinaia e privando queste ultime della loro consonante finale.
Tiebair=novecentodieci; miefaic=cinquecentoventi; sietaiz=ottocentonovanta;
fiekaid=duecentotrenta; piebair=seicentodieci.
6) I numeri formati da centinaia, decine e unit si ottengono, aggiungendo le unit alle decine e privando le decine e le centinaia della loro consonante finale.
Tiepailig=novecentosessantaquattro; liemaikid=quattrocentocinquantatre; piebaitiz=seicentodiciannove; miepailig=cinquecentosessantaquattrro; sietaibir=ottocentonovantuno; fiebaikid=duecontotredici; liefaific=quattrocentoventidue..
7) Dopo il 999, si ricorre al 1000 (vieb). Va fatto presente che negli ordini dal 1.000 in poi (come 10.000, 100.000, 1.000.000, ecc ), i quali sono tutti potenze del 10 e sono formati sempre da quattro lettere, la consonante finale indica una o pi terne di zeri da considerare nel numero, essendo esse consonanti numeriche, il cui valore ci ben noto. Inoltre, le consonanti c e z rappresentano rispettivamente uno zero e due zeri da aggiungersi al valore delle terne.
Se prendiamo vieb, ossia mille, la consonante numerica b (1) ci dice che gli zeri da aggiungere all unit sono tre (1x3). Non ci sono altri zeri da aggiungere, poich in esso mancano sia la consonante c (uno zero) sia la consonante z (due zeri). Infine i vari ordini vengono separati con un trattino. Ecco alcuni esempi:
Mille e due=vieb-fic; diecimila e quaranta=ciob-laig; centomila e trecento=ziub-kied; un milione=vief; un milione e trenta=vief-kaid; un milione e centomila=vief-ziub; un milione e centoquaranta=vief-bielaig; un milione e diecimilaquattro=vief-ciob-lig;
un miliardo e novanta=viek-taiz; dieci miliardi e un milionecinque=ciok-vief-mih; cento miliardi diecimilasettanta=ziuk-vief-raiv;
un bilione=viel; dieci bilioni e ottocentotre=ciol-siekid; centobilioni, diecimilioni e novecento=ziul-ciof-tiez;
un biliardo=viem; diecibiliardi=ciom; centobiliardi=zium; un biliardo, dieci miliardi e diecimila=viem-ciok-ciob;
un trilione=viep; dieci trilioni, cento biliardi e diecimila=ciop-zium-ciob; cento trilioni, dieci miliardi e centomilasettanta=ziup-ciok-ziub-raiv;
un triliardo=vier; cento triliardi, diecimilioni e centomila=ziur-ciof-ziub; un biliardo, dieci miliardi e centomila=viem-ciok-ziub;
un quadrilione=vies; dieci quadrilioni, cento bilioni, un milione e mille=cios-ziul-vief-vieb; cento quadrilioni, cento triliardi, diecibilioni e dieci milioni=zius-ziur-ciol-ciof;
un quadriliardo=viet; dieci quadriliardi, dieci trilioni e un miliardo=ciot-ciop-viek.
8) Gli ordini, dalle migliaia in poi, a volte sono preceduti dai numeri 2-999, che ne indicano la quantit . In quel caso tali numeri prendono il suffisso, che viene dato dalle ultime due cifre della potenza del 10 a cui si riferisce. L unione, comunque, avviene tramite la vocale i. Adesso vedremo come avviene con vari esempi.
Tremila=kidieb (dove kid 3 e eb la parte terminale di vieb (mille);
quarantotto milioni=laisixief (dove laisix=48, mentre ef la parte terminale di vief=un milione);
cinquantasei miliardi=maipiniok (dove maipin=56, mentre ek la parte terminale di viek=miliardo);
ottocentodieci bilioni=siebairiel (dove siebair=810, mentre el la parte terminale di iel=bilione);
duemilaquattrocento triliardi=ficieb-liegier (dove ficieb=2000, mentre eb la parte terminale di vieb=mille e er la parte terminale di
vier=triliardo)
9) Nella Raubser, i numeri hanno anche una forma letterale, che pu sostituire quella delle cifre. Le lettere, che vanno scritte in stampatello
maiuscolo, rappresentano le consonanti iniziali delle dieci cifre da 0 a 9. Essa riesce molto abbreviata, come possiamo renderci conto dai
seguenti esempi:
TFM=novecentoventicinque; BL=quattordici; SVR=ottocentosette; KP=trentasei; PKT=seicentotrentanove; FVS=duecentootto; FBV=duecentodieci;
TTT=novecentonovantanove; LBM=quattrocentoquindici.
Dal mille in poi, ogni ordine, dal pi grande al pi piccolo, viene indicato dalle due ultime lettere del suo nome (una vocale pi una
consonante). Inoltre, gli ordini vengono separati l uno dall altro con un trattino (-).
MEf=cinquemilioni; MOF=cinquantamilioni; MuF=cinquecentomilioni; KLREB-MFV=trecentoquarantasettemilacinquecentoventi;
KPEK-FVEF=trentaseimiliardi e ventimilioni; MFEK-SKEF-PEB=cinquantaduemiliardi, ottantatremilioni, seimilamila; REL-FEB-KLV=settebilioni,
duemila, trecentoquaranta; ecc
18) Numeri oltre i Miliardi
I Numeri oltre i Miliardi, che si possono esprimere con un nome, raggiungono grandezze superastronomiche. Basti pensare che il pi grande di essi, bitutit, rappresenta 104999, cio 1 seguito da 4999 zeri. Al riguardo, bisogna sapere che la formazione di tali numeri e l in terpretazione del loro valore si presen tano l una semplice e l altra agevole, per il fatto che essi sono stati ottenuti seguendo un criterio aritmetico basato sulla pura logica matematica. Perci cerchiamo di approfondire bene tale criterio. Ma, prima di continuare il discorso su tale argomento, ci conviene rivedere quanto gi appreso in precedenza. Ebbene, nei numeri potenze del 10 oltre i Miliardi, con esponente fino a 99, il bi iniziale indica la base 10; la sillaba che segue, la quale pu essere vi, bi, fi, ki, li mi, pi, ri, si, ti, indica le centinaia (il suo valore dato dalla consonante numerica); il numero formato dalle due consonanti numeriche finali, aggiunto alle centinaia, ci d<à l'esponente della base 10. In tali numeri e negli altri che seguiranno, l'accento cade sulla terzultima vocale. Vediamo alcuni esempi:
bivivif=102; bvibis=1018; bivifil=1024; bivikiv=1030; bivikip=1036; bivilif=1042; bivilis=1048; bivimil=1054; bivitit=1099.
bibivik=10103; bibifir=10127; bibilim=10145; bibimit=10159; bibiriv=10170; bibikil=10134; bibibip=10116; bibipis=10168; bibiviv=10100; bibisir=10187; bibitit=10199.
bifivis=10208;bififip=10226;bifilip=10246;bifipiv=10260; bifirib=10271;bifikim=10235;bifibir=10217;bifipit=10269;bifiviv=10200;bifisis=10288;bifitit=10299.
bikivib=10301;bikifis=10328;bikilip=10346;bikipiv=10360;bikirib=10371;bikikim=10335;bikibir=10317;bikipit=10369;bikitif=10392;bikitit=10399.
bilivil=10404;bilifis=10428;bililip=10446;bilipiv=10460;bilirib=10471;bilikim=10435;bilibir= 10417;bilipip=10466;bilitif=10492;bilitit=10499.
bimivif=10502;bimibis=10518;bimifil=10524;bimikiv=10530;bimikip=10536;bimilif=10542;bimilis=10548;bimimil=10554;bimitit=10599.
bipivik=10603;bipifir=10627;bipilim=10645;bipimit=10659;bipiriv=10670;bipikil=10634;bipibip=10616;bipipis=10668;bipiviv=10600;bipisir=10687;bipitit=10699.
birivis=10708;birifip=10726;birilip=10746;biripiv=10760;biririb=10771;biri kim=10735;biribir=10717;biripit=10769;biriviv=10700;birisis=10788;biritit=10799.
bisivib=10801;bisifis=10828;bisilip=10846;bisipiv=10860;bisirib=10871;bisikim=10835;bisibir=10817;bisipit=10869;bisitif=10892;bisitit=10899.
bitivil=10904;bitifis=10928;bitilip=10946;bitipiv=10960;bitirib=10971;bitikim=10935;bitibir=10917;bitipip=10966;bititif=10992;bititit=10999.
In tali numeri vi, bi, fi, ki, li, mi, pi, ri, si e ti indicano le centinaia, poich corrispondono rispettivamente a 0, 100, 200, 300, 400, 500, 600, 700, 800 e 900. Ma, se alla i sostituiamo la a, facendoli diventare va, ba, fa, ka, la, ma, pa, ra, sa e ta, il loro valore aumenta di un migliaio, per cui essi diventano rispettivamente 1000, 1100, 1200, 1300, 1400, 1500, 1600, 1700, 1800 e 1900. Vediamo alcuni esempi:
b vabis=101018;b bafir=101127;b fasis=101288;b kalip=101346;b larib=101471;b mamil= 101554;b parib=101671;b rarib=101771;b sakim=101835;b tatit= 101999.
Se invece alla i sostituiamo la e e li facciamo diventare ve, be, fe, ke, le, me, pe, re, se e te, il loro valore aumenta di due migliaia, per cui essi diventano rispettivamente 2000, 2100, 2200, 2300, 2400, 2500, 2600, 2700, 2800 e 2900. Vediamo alcuni esempi:
bivebis=102018;bibefir=102127;bifesis=102288;bikelip=102346;bilerib=102471;bimemil=102554;biperib=102671;birerib=102771;bisekim=102835;bitetit=102999.
Se invece alla i sostituiamo la o e li facciamo diventare vo, bo, fo, ko, lo, mo, po, ro, so e to, il loro valore aumenta di tre migliaia, per cui essi diventano rispettivamente 3000, 3100, 3200, 3300, 3400, 3500, 3600, 3700, 3800 e 3900. Vediamo alcuni esempi:
bivobis=103018;bibofir=103127;bifosis=103288;bikolip=103346;bilorib=103471;bimomil=103554;bioerib=1023671;birorib=103771;bisokim=103835;bitotit=103999.
Se invece alla i sostituiamo la u e li facciamo diventare vu, bu, fu, ku, lu, mu, pu, ru, su e tu, il loro valore aumenta di quattro migliaia, per cui essi diventano rispettivamente 4000, 4100, 4200, 4300, 4400, 4500, 4600, 4700, 4800 e 4900. Vediamo alcuni esempi:
bivubis=104018;bibufir=104127;bifusis=104288;bikulip=104346;bilurib=104471;bimumil=104554;bipurib=104671;birurib=104771;bisukim=104835;bitutit=104999.
Se al posto di 1 c' un numero diverso, abbiamo:
Kid tao bivibik=3x1013 o 3 seguito da 13 zeri; riv tao bivibif=7x1012 o 7 seguito da 12 zeri; baif c tao bivibim=12x1015 o 12 seguito da 15 zeri; pin tao bivibis=6x1018 o 6 seguito da 18 zeri; ecc
Nelle potenze con base diversa da 10, abbiamo:
kid-xeibik=313; mih-xeivik=53; riv-xeibiv=710; baisix-xeivit=189.
(Come si vedr in seguito, il prefisso xei deriva da xeuz=potenza)
Oltre al nome, le potenze del 10 o di altri numeri, possono avere una forma letterale, che si ottiene nel modo seguente:
104=BVl; 93=Tk; 28=Fs; 10325=BVkfm; 10-25=BV-fm; 37x1032=KRxBVkf.
|
Misura |
Valore |
Prefisso |
Simbolo |
|
voic=decimo |
10-1 |
voi |
vc |
|
vuiz=centesimo |
10-2 |
vui |
vz |
|
beiv=millesimo |
10-3 |
bei |
bv |
|
boic=decimillesimo |
10-4 |
boi |
bc |
|
buiz=centimillesimo |
10-5 |
bui |
bz |
|
feiv=milionesimo |
10-6 |
fei |
fv |
|
foic=decimilionesimo |
10-7 |
foi |
fc |
|
fuiz=centimilionesimo |
10-8 |
fui |
fz |
|
keiv=miliardesimo |
10-9 |
kei |
kv |
|
koic=decimiliardesimo |
10-10 |
koi |
kc |
|
kuiz=centimiliardesimo |
10-11 |
kui |
kz |
|
leiv=bilionesimo |
10-12 |
lei |
lv |
|
loic=decibilionesimo |
10-13 |
loi |
lc |
|
luiz=centibilionesimo |
10-14 |
lui |
lz |
|
meiv=biliardesimo |
10-15 |
mei |
mv |
|
moic=decibiliardesimo |
10-16 |
moi |
mc |
|
muiz=centibiliardesimo |
10-17 |
mui |
mz |
|
peiv=trilionesimo |
10-18 |
pei |
pv |
|
poic=decitrilionesimo |
10-19 |
poi |
pc |
|
puiz=centitrilionesimo |
10-20 |
pui |
pz |
|
reiv=triliardesimo |
10-21 |
rei |
rv |
|
roic=decitriliardesimo |
10-22 |
roi |
rc |
|
ruiz=centitriliardesimo |
10-23 |
rui |
rz |
|
seiv=quadrilionesimo |
10-24 |
sei |
sv |
|
soic=deciquadrilionesimo |
10-25 |
soi |
sc |
|
suiz=centiquadrilionesimo |
10-26 |
sui |
sz |
|
teiv=quadriliardesimo |
10-24 |
tei |
tv |
|
toic=deciquadriliardesimo |
10-25 |
toi |
tc |
|
tuiz=centiquadriliardesimo |
10-26 |
tui |
tz |

LA MIA MATEMATICA
A) GEOMETRIA
1) Nuovi Teoremi sul Triangolo Rettangolo
2) Risoluzione algebrica del teorema di Pitagora
3) Teoremi geometrici al posto di Equazioni di II grado
4) Teorema sulle proiezioni dei cateti
5) Terne Pitagoriche Primitive e multiple: come ottenerle
6) Terne pitagoriche entro il 1000
B) ARITMETICA
7) Come ottenere i Numeri Primi
8) Dai multipli del 6 ai Numeri Primi
9) Sui Quadrati dei Numeri Interi
10) Sui Cubi dei Numeri Interi
11) Il Mediano e i suoi Simmetrici
12) Radice dei Quadrati dei Numeri da 11 a 99
13) Radice dei Cubi dei Numeri da 11 a 99
14) Moltiplicazioni dirette mediante il grafico
15) Moltiplicazioni per 11
16) Nuovo Sistema Numerico in Lettere
17) I Numeri: dalle unit ai Miliardi
18) Numeri oltre i Miliardi
19) Nomi dei Multipli e dei Sottomultipli delle Potenze del 10
20) unit Fondamentali di Misura e loro Simboli
21) Sistema Metrico Decimale
22) Tabella delle potenze del 10 fino all'esponente 1000
_______________________________________________________
A) GEOMETRIA
1) Nuovi teoremi sul triangolo rettangolo
Teorema 1

Il rettangolo costruito sui cateti AB e BC, ossia ABCD, è equivalente al rettangolo costruito sulla somma dei cateti BF e il lato del quadrato BH, ossia BFGH. Per cui, indicando con a e b il cateto maggiore e quello minore, con l il lato e con d la diagonale del quadrato o bisettrice del triangolo rettangolo, avremo:
ABCD ~ BFGH; da cui:
![]()
PROBLEMI
Nel triangolo rettangolo ABC, i cateti BC (a) e BA (b) misurano rispettivamente 28 cm e 21 cm. Calcolare il lato del quadrato inscritto l e la
diagonale d.
![]()
Nel triangolo rettangolo ABC, l'area misura 294 cm² e il lato del quadrato misura 12 cm. Calcolare la somma dei cateti.
![]()
Nel triangolo rettangolo ABC, la somma dei cateti misura 49 cm e il lato del quadrato misura 12 cm. Calcolare l'area.
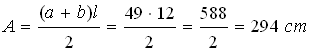 quadrati
quadrati
Nel triangolo rettangolo ABC, la somma dei cateti misura 49 cm e l'area misura 294 cm². Calcolare il lato del quadrato e la sua diagonale.
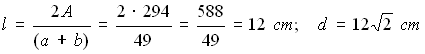
Teorema 2
 Il
rettangolo costruito sulle differenze tra ogni cateto e il lato del quadrato,
ossia LRDP, è equivalente al quadrato inscritto nel triangolo, ossia
BHLM. Ciò vuol dire che il lato del quadrato medio proporzionale tra tali
differenze AH e CM. Per cui, indicandole con x (la minore)
e con y (la maggiore), avremo:
Il
rettangolo costruito sulle differenze tra ogni cateto e il lato del quadrato,
ossia LRDP, è equivalente al quadrato inscritto nel triangolo, ossia
BHLM. Ciò vuol dire che il lato del quadrato medio proporzionale tra tali
differenze AH e CM. Per cui, indicandole con x (la minore)
e con y (la maggiore), avremo:
LRDP ~ BHLM; da cui:
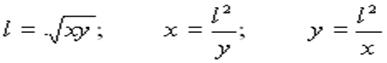
PROBLEMI
Nel triangolo rettangolo ABC, x e y misurano rispettivamente 9 cm e 16 cm. Calcolare il lato del quadrato inscritto.
![]()
Nel triangolo rettangolo ABC, il lato del quadrato misura 12 cm e y misura 16
cm. Calcolare la misura di x.
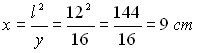
Nel triangolo rettangolo ABC, il lato del quadrato misura 12 cm e x misura 9 cm.
Calcolare la misura di y.
![]()
Teorema 3

Il rettangolo costruito sulla somma dei cateti (BC+ BA) e la somma delle loro differenze (HA+MC) è equivalente al quadrato costruito sull ipotenusa AC. Ciò vuol dire che l ipotenusa media proporzionale tra tali somme. Per cui, indicando con a e b il cateto maggiore e quello minore, con c l&asop;ipotenusa, con x e y rispettivamente la differenza minore e quella maggiore, avremo:
BC+BA) (AH+CM) ~ AC AC; da cui:
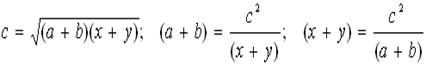
PROBLEMI
Nel triangolo rettangolo ABC, i cateti misurano 28 cm e 21 cm, mentre y e x
misurano rispettivamente 16 cm e 9 cm. Calcolare l'ipotenusa.
![]()
Nel triangolo ABC, l'ipotenusa misura cm 35, mentre la somma di y + x misura 25
cm. Calcolare la somma dei cateti.
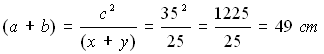
Nel triangolo ABC, l'ipotenusa misura cm 35, mentre la somma dei cateti misura
49 cm. Calcolare la somma di y + x.
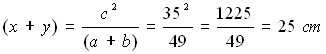
Teorema 4
 Il
quadrato di ciascun cateto equivalente al rettangolo costruito sulla somma dei
cateti BC+BA e la relativa differenza AH o CM. Per
cui, indicando con a e b rispettivamente il cateto maggiore e
quello minore, con c l ipotenusa, con x e y la differenza
minore e quella maggiore, avremo:
Il
quadrato di ciascun cateto equivalente al rettangolo costruito sulla somma dei
cateti BC+BA e la relativa differenza AH o CM. Per
cui, indicando con a e b rispettivamente il cateto maggiore e
quello minore, con c l ipotenusa, con x e y la differenza
minore e quella maggiore, avremo:
(BC+BA) MC ~ BC ; da cui:
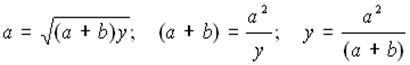
PROBLEMA
Nel triangolo rettangolo ABC, i cateti a e b misurano rispettivamente 28 cm e 21 cm. Calcolare le misure di x e di y.
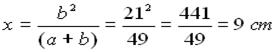
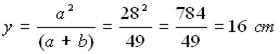
Teorema 5
 Ogni
cateto medio proporzionale tra la somma dei cateti e la relativa differenza.
Per cui, indicando con a e b il cateto maggiore e quello minore, con x e y la
differenza minore e quella maggiore, avremo:
Ogni
cateto medio proporzionale tra la somma dei cateti e la relativa differenza.
Per cui, indicando con a e b il cateto maggiore e quello minore, con x e y la
differenza minore e quella maggiore, avremo:
(BC+BA) HA ~ BA ; da cui:
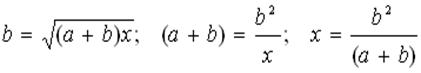
PROBLEMA
Nel triangolo rettangolo ABC, la somma dei cateti misura 49 cm, mentre y e x
misurano rispettivamente 16 cm e 9 cm. Calcolare i cateti.
![]()
![]()
Teorema 6
 Il
rettangolo costruito sul cateto maggiore, ossia BC, e l ipotenusa AC
equivalente al rettangolo costruito sulla somma dei cateti BC+BA
e la parte minore dell ipotenusa che viene divisa dalla bisettrice, ossia LA.
Per cui, indicando con a e b il cateto maggiore e quello minore,
con c l ipotenusa e con z il segmento maggiore dell ipotenusa,
avremo:
Il
rettangolo costruito sul cateto maggiore, ossia BC, e l ipotenusa AC
equivalente al rettangolo costruito sulla somma dei cateti BC+BA
e la parte minore dell ipotenusa che viene divisa dalla bisettrice, ossia LA.
Per cui, indicando con a e b il cateto maggiore e quello minore,
con c l ipotenusa e con z il segmento maggiore dell ipotenusa,
avremo:
BA AC ~ (BC+BA) LA; da cui:
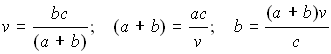
PROBLEMI
Nel triangolo rettangolo ABC, i cateti a e b misurano rispettivamente 28 cm e 21 cm, mentre l'ipotenusa misura 35 cm. Calcolare la misura di v.
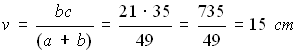
Nel triangolo rettangolo ABC, la somma dei cateti misura 49 cm, l'ipotenusa misura 35 cm, mentre v misura 15 cm. Calcolare il cateto minore.
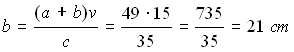
Teorema 7
 Il
rettangolo costruito sul cateto maggiore, ossia BC, e l'ipotenusa AC
è equivalente al rettangolo costruito sulla somma dei cateti BC+BA
e la parte maggiore dell'ipotenusa che viene divisa dalla bisettrice, ossia
LC. Per cui, indicando con a e b il cateto maggiore e quello
minore, con c l'ipotenusa e con z il segmento maggiore, avremo:
Il
rettangolo costruito sul cateto maggiore, ossia BC, e l'ipotenusa AC
è equivalente al rettangolo costruito sulla somma dei cateti BC+BA
e la parte maggiore dell'ipotenusa che viene divisa dalla bisettrice, ossia
LC. Per cui, indicando con a e b il cateto maggiore e quello
minore, con c l'ipotenusa e con z il segmento maggiore, avremo:
BC AC ~ (BC+BA) LC; da cui:
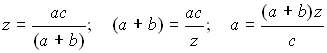
PROBLEMI
Nel triangolo rettangolo ABC, i cateti a e b misurano rispettivamente 28 cm e 21 cm, mentre l'ipotenusa misura 35 cm. Calcolare la misura di z.
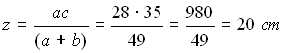
Nel triangolo rettangolo ABC, la somma dei cateti misura 49 cm, l'ipotenusa
misura 35 cm, mentre z misura 20 cm. Calcolare il cateto maggiore.
![]()
Teorema 8

Il rettangolo costruito sul cateto minore BA e il lato del quadrato BM, ossia ABMR, è equivalente al rettangolo costruito sul cateto maggiore BC e la differenza tra il cateto minore e il lato del quadrato AH, ossia AHPD. Perciò avremo:
ABMR = AHPD; da cui:
![]()
Nel triangolo rettangolo ABC, il cateto minore misura 21 cm e x misura 9 cm. Calcolare il cateto maggiore.
![]()
Nel triangolo rettangolo ABC, i cateti misurano 28 cm e 21 cm, mentre il lato
del quadrato inscritto misura 12 cm. Calcolare la misura di x.
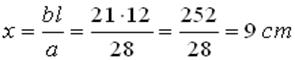
Teorema 9

Il rettangolo costruito sul cateto maggiore BC e il lato del quadrato BH, ossia HBCP, è equivalente al rettangolo costruito sul cateto minore AB e la differenza tra il cateto maggiore BC e il lato del quadrato BM, ossia CDRM. Perci avremo:
HBCP = CDRM ; da cui:
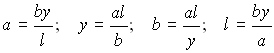
PROBLEMI
Nel triangolo rettangolo ABC, il cateto maggiore misura 28 cm e y misura 16 cm. Calcolare il cateto minore.
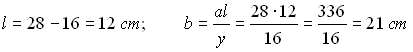
Nel triangolo rettangolo ABC, i cateti misurano 28 cm e 21 cm, mentre il lato del quadrato inscritto misura 12 cm. Calcolare la misura di y.
![]()
2) RISOLuZIONE ALGEBRICA DEL TEOREMA DI PITAGORA
1) In algebra si è studiato il seguente prodotto notevole:
(a-b)2 = a2 + b2 - 2ab; da cui:
2ab + (a-b)2 = a2 + b2
dove:
a e b = cateto maggiore e cateto minore;
2ab= doppio rettangolo costruito sui cateti o doppio prodotto dei cateti;
ab= rettangolo costruito sui cateti o prodotto dei cateti;
(a-b)2 = quadrato della differenza dei cateti;
a2+b2 = quadrato dell'ipotenusa, in quanto somma dei quadrati dei due cateti;
ma dalla seconda uguaglianza sopra riportata, si deduce che il quadrato dell'ipotenusa è dato anche da:
2ab + (a-b)2
Per cui l'ipotenusa è anche uguale al doppio prodotto dei cateti più il quadrato della loro differenza.
Comunque, geometricamente parlando, possiamo dire che il quadrato dell'ipotenusa è equivalente al doppio rettangolo costruito sui cateti più il quadrato costruito sulla differenza degli stessi.
Così, indicando con a, b, c rispettivamente il cateto maggiore, il cateto minore e l'ipotenusa, avremo:
![]()
Ma abbiamo anche:
![]()
Se abbiamo a=12 e b=5, c sarà uguale a:
![]()
![]()
2) In algebra abbiamo ancora il seguente prodotto notevole:
a2-b2 = (a + b) (a b);
dove:
a e b = cateto maggiore e cateto minore;
(a + b) = somma dei cateti;
(a b) = differenza dei cateti;
a2+b2 = quadrato dell'ipotenusa
Per il teorema di Pitagora, il quadrato di un cateto è uguale al quadrato dell'ipotenusa meno il quadrato dell'altro cateto.
Indicando con c l'ipotenusa, abbiamo:
a2 = c2 b2; b2 = c2 a2
Così, indicando con a, b, c rispettivamente il cateto maggiore, il cateto minore e l'ipotenusa e applicando il prodotto notevole sopra riportato, avremo:
a2 = (c + b) (c b);
b2 = (c + a) (c a);
Per cui il quadrato di un cateto è uguale al prodotto tra la somma dell'ipotenusa più l'altro cateto e la loro differenza.
![]()
![]()
In un triangolo rettangolo, se l'ipotenusa misura 25 cm e il
cateto minore misura 7 cm, il cateto maggiore sarà uguale a:
![]()
In un triangolo rettangolo, se l'ipotenusa misura 25 cm e il
cateto maggiore misura 7 cm, il cateto minore sarà uguale a:
![]()
3) TEOREMI GEOMETRICI AL POSTO DI SISTEMI DI EQuAZIONE DI SECONDO GRADO
Nel triangolo rettangolo, alcuni problemi possono essere risolti, ricorrendo a teoremi geometrici ed evitando sistemi di equazione di secondo grado.
Il primo teorema è il seguente:
Il quadrato della somma dei cateti (a+b) più quello della loro differenza (a-b) danno il doppio quadrato dell'ipotenusa 2c .
La sua applicazione si ha nei seguenti tre problemi:
1) In un triangolo rettangolo, l'ipotenusa misura 20 cm e la somma dei cateti misura 28 cm. Calcolare i cateti.
![]()
Sommando poi la somma dei cateti e la loro differenza e dividendo per 2 il risultato, otteniamo il cateto maggiore.
a = (28 + 4) : 2 = 32 : 2 = 16 cm
Sottraendo poi la differenza dei cateti alla loro somma e dividendo per 2 il risultato, otteniamo il cateto minore.
b
= (28 - 4) : 2 = 24 : 2 = 12 cm
2) In un triangolo rettangolo, l'ipotenusa misura 17 cm e la differenza dei cateti misura 7 cm. Calcolare i cateti.
![]()
Sommando poi la somma dei cateti e la loro differenza e dividendo per 2 il risultato, otteniamo il cateto maggiore.
a = (23 + 7) : 2 = 30 : 2 = 15 cm
Sottraendo poi la differenza dei cateti alla loro somma e dividendo per 2 il risultato, otteniamo il cateto minore.
b = (23 - 7) : 2 = 16 : 2 = 8 cm
3) In un triangolo rettangolo, la somma dei cateti misura 31 cm e la differenza dei cateti misura 17 cm. Calcolare l'ipotenusa.
![]()
![]()
Il secondo teorema è il seguente:
Il doppio prodotto dei cateti 2ab più il quadrato della loro differenza (a-b) danno il quadrato dell'ipotenusa.
La sua applicazione si ha nei seguenti tre problemi:
1) In un triangolo rettangolo, l'ipotenusa misura 5 cm e l'area misura 6 cm². Calcolare i due cateti.
![]()
Applicando il teorema 1, avremo la somma dei cateti:
![]()
Conoscendosi la loro somma e la loro differenza, come già visto, i cateti saranno:
a = (7 + 1) : 2 = 8 : 2 = 4 cm ;
b = (7 - 1) : 2 = 6 : 2 = 3 cm
2) In un triangolo rettangolo, l'ipotenusa misura 10 cm, mentre la differenza dei cateti misura 2 cm. Calcolare l'area.
A = (10² - 2²) : 4 = (100 - 4) : 4 = 96 : 4 = 24 cm²
3) In un triangolo rettangolo, l'area misura 30 cm², mentre la differenza dei cateti misura 7 cm. Calcolare l'ipotenusa c.
![]()
4) TEOREMA SuLLE PROIEZIONI DEI CATETI

In un triangolo rettangolo, la differenza dei quadrati delle proiezioni dei cateti sull'ipotenusa equivalente al rettangolo che ha per dimensioni la somma e la differenza dei cateti.
CH2 AH2 = (BC + AB) (BC - AB)
Per cui le formule inverse risultano:
BC + AB = (CH2 AH2) : (BC AB)
BC - AB = (CH2 AH2) : (BC + AB)
CH2 = (BC + AB) (BC - AB) + AH2
AH2 = CH2 - (BC + AB) (BC - AB)
PROBLEMI
1) In un triangolo rettangolo, i cateti misurano 40 cm e 30 cm. Calcolare la differenza dei quadrati delle proiezioni dei cateti sull'ipotenusa.
CH2 AH2 = (BC+AB) (BC-AB) = (40+30) (40 30) = 70 10 = 700 cm2
2) In un triangolo rettangolo, le proiezioni dei cateti sull'ipotenusa misura 32 cm e 18 cm, mentre la somma dei cateti misura 70 cm. Calcolare i due cateti.
BC-AB =(CH2 AH2) : (BC+AB)=(322 182) : (40+30)=(1024 324) : 70=700 : 70=10 cm
BC= (70 + 10) : 2 = 80 : 2 = 40 cm
AB = (70 10) : 2 = 60 : 2 = 30 cm
3) In un triangolo rettangolo, le proiezioni dei cateti sull'ipotenusa misura 32 cm e 18 cm, mentre la differenza dei cateti misura 10 cm. Calcolare i due cateti.
BC + AB = (CH2 AH2) : (BC - AB) = (322 182) : (40-30) = (1024 324) : 10 = 700 : 10 = 70 cm
BC= (70 + 10) : 2 = 80 : 2 = 40
AB = (70 10) : 2 = 60 : 2 = 30
4) In un triangolo rettangolo, i cateti misurano 20 cm e 15 cm, mentre la proiezione del cateto minore sull'ipotenusa misura 9 cm. Calcolare la proiezione del cateto maggiore sull'ipotenusa.
CH2=(BC+AB) (BC-AB)+AH2=(20+15)
(20-15) + 92
= 35 5 + 81 = 175+81 = 256, la cui radice quadrata è 16 cm;
5) In un triangolo rettangolo, i cateti misurano 20 cm e 15 cm, mentre la proiezione del
cateto maggiore sull'ipotenusa misura 16 cm. Calcolare la proiezione del cateto
minore sull'ipotenusa.
AH2
= (BC+AB) (BC-AB) (BC+AB)
(BC-AB) + AH2
= (20+15) (20-15) + 92 = 35 5 + 81=175 + 81 = 256; la cui radice quadrata è 16 cm
AH2 = CH2 - (BC+AB) (BC-AB) = 162 - (20+15)(20-15) =
256-35 5 = 256-175 = 81; la cui radice quadrata è 9 cm
Formano una terna pitagorica tre numeri interi, che rappresentano
i lati di un triangolo rettangolo e soddisfano il teorema di Pitagora, nel senso
che la somma dei quadrati dei due più piccoli è equivalente al quadrato del più
grande. Comunque, siccome abbiamo visto che un lato di un triangolo rettangolo,
conoscendo gli altri due, può essere trovato anche senza applicare il teorema di
Pitagora, è improprio chiamarla terna pitagorica, anziché terna di un triangolo
rettangolo.
Gli autori di
testi di Geometria, nei problemi con applicazione del teorema di Pitagora, per
avere risultati interi, ricorrono spesso a tali terne, che per lo più sono
sempre le stesse, come le terne prime: 3, 4 e 5; 5, 12 e 13; 7, 24 e 25; 8, 15 e
17. Da ognuna di esse, si possono poi ricavare infinite terne multiple. Basta
moltiplicare i loro tre numeri per uno stesso numero intero, a cominciare dal 2
fino all infinito. Per questo ogni terna prima ha una infinità di terne
multiple.
Esempio:
Dalla terna
prima 3, 4 e 5, possiamo avere le terne multiple: 6, 8 e 10; 9, 12 e 15; 12, 16
e 20; 15, 20 e 25; 18, 24 e 30; 21, 28 e 35; 24, 32 e 40; 27, 36 e 45; 30, 40 e
50; 33, 44 e 55; ecc...
Anche le terne
prime di un triangolo rettangolo sono infinite e si possono ricavare facilmente,
applicando le due seguenti regole:
A) Se si parte
da un numero dispari, che viene considerato cateto minore, abbiamo il seguente
procedimento:
Si ricavano
dal cateto minore i due numeri consecutivi, la cui somma dà il cateto stesso.
Dal numero 3 si ricavano 1 e 2; dal numero 5 si ricavano 2 e 3; dal numero 7 si
ricavano 3 e 4. La stessa cosa vale per tutti gli altri numeri dispari
successivi.
Ebbene, il
cateto maggiore è dato dal prodotto di uno dei due numeri ricavati (conviene
sempre raddoppiare il minore) per il doppio dell'altro; mentre l'ipotenusa `
data da tale prodotto pi 1.
Nel caso A),
si hanno solo terne primitive.
Così, per
trovare il cateto maggiore e l'ipotenusa, si hanno le due seguenti espressioni
aritmetiche:
Se il cateto
minore è 3 (1+2), abbiamo:
cateto
maggiore: 2 + 2 = 4
ipotenusa: 2 +
2 + 1 = 5
Se il cateto
minore è 5 (2+3), abbiamo:
cateto
maggiore: 4 x 3 = 12
ipotenusa: 4 x
3 + 1 = 13
Se il cateto
minore è 7 (3+4), abbiamo:
cateto
maggiore: 6 x 4 = 24
ipotenusa: 6 x
4 +1 = 25
B) Se si parte
da un numero pari, che viene considerato cateto minore, abbiamo il seguente
procedimento:
Si ricavano
dal cateto minore i due numeri alternati, la cui somma dà il cateto stesso. Dal
numero 4 si ricavano 1 e 3; dal numero 6 si ricavano 2 e 4; dal numero 8 si
ricavano 3 e 5; dal numero 10 si ricavano 4 e 6; dal numero 12 si ricavano 5 e
7. La stessa cosa vale per tutti gli altri numeri dispari successivi.
Ebbene, il
cateto maggiore è dato dal prodotto dei due numeri ricavati; mentre l'ipotenusa
è data da tale prodotto più 2.
Nel caso B),
si hanno sia terne primitive, cioè quelle ottenute da 4 e dai suoi multipli, sia
terne derivate, cioè tutte le altre.
Così, per
trovare il cateto maggiore e l'ipotenusa, si hanno le due seguenti espressioni
aritmetiche:
Se il cateto
minore è 4 (1+3), abbiamo:
cateto
maggiore: 1 x 3 = 3
ipotenusa: 1 x
3 + 2 = 5
(Si tratta
dell'unico caso in cui 4 risulta cateto maggiore, anziché cateto minore, poiché
esso viene a coincidere con la terna ricavata dal numero dispari 3, il quale dà:
3-4-5)
Se il cateto
minore è 6 (2+4), abbiamo:
cateto
maggiore: 2 x 4 = 8
ipotenusa: 2 x
4 + 2 = 10
(terna
multipla di 3-4-5)
Se il cateto
minore è 8 (3+5), abbiamo:
cateto
maggiore: 3 x 5 = 15
ipotenusa: 3 x
5 + 2 = 17
(terna
primitiva)
Se il cateto
minore è 10 (4+6), abbiamo:
cateto
maggiore: 4 x 6 = 24
ipotenusa: 4 x
6 + 2 = 26
(terna
multipla di 5-12-13)
Se il cateto
minore è 12 (5+7), abbiamo:
cateto
maggiore: 5 x 7 = 35
ipotenusa: 5 x
7 + 2 = 37
(terna
primitiva)
Come possiamo
osservare, se i due numeri alternati risultano dispari (solo nei multipli di 4),
essi danno luogo ad una terna primitiva; se invece risultano pari, danno luogo
ad una terna derivata).
C) Se di un
triangolo rettangolo si conoscono i due cateti oppure il cateto minore e
l'ipotenusa, per sapere se essi formano una terna pitagorica, bisogna procedere,
come se stessimo ricavando dal cateto minore quello maggiore o l'ipotenusa. Se
il procedimento ci porta allo stesso cateto maggiore noto o all'ipotenusa nota,
essi formano una terna pitagorica.
Se i cateti
sono 5 e 12, siccome 5 è uguale a 2+3 e il prodotto 4x3 dà 12, i cateti 5 e 12
fanno parte di una terna pitagorica.
Se 5 e 13 sono
rispettivamente il cateto minore e l'ipotenusa, siccome 5 è uguale a 2+3 e il
risultato di 4x3+1 dà 13, 5 e 13 fanno parte di una terna pitagorica.
Se i cateti
sono 8 e 15, siccome 8 è uguale a 3+5 e il prodotto 3x5 dà 15, i cateti 8 e 15
fanno parte di una terna pitagorica.
Se 8 e 15 sono
rispettivamente il cateto minore e l'ipotenusa, siccome 8 à uguale a 3+5 e il
risultato di 3x5+2 dà 17, 8 e 17 fanno parte di una terna pitagorica.
D) Esiste una
certa progressione aritmetica nelle terne primitive, siano esse derivate da
numeri dispari o da numeri pari multipli di 4. La quale è la seguente:
Il cateto
maggiore di una terna primitiva è dato dal cateto minore della terna più la
somma dei cateti della precedente terna.
Esempi:
Se abbiamo la
terna 3, 4 e 5, che è la terna ottenuta con 3, il cateto maggiore della terna di
5 si ottiene, aggiungendo a 5 la somma dei due cateti della terna di 3:
5+7 (3+4) = 12
Per ottenere
l'ipotenusa, si aggiunge sempre una unit al cateto maggiore: 12+1=13.
Se abbiamo la
terna 8, 15 e 17, che è la terna ottenuta con 8, il cateto maggiore della terna
di 12 si ottiene, aggiungendo a 12 la somma dei cateti della terna di 8:
12+23 (8+15) =
35
Per ottenere
l'ipotenusa, si aggiungono sempre due unità al cateto maggiore: 35+2=37.
una
progressione di questo tipo ci permette di ottenere più velocemente le terne
primitive di più numeri in successione, senza ricorrere ogni volta alle due
regole riportate sopra, dopo che si è ottenuta la prima.
(Le terne
pitagoriche in neretto sono primitive)
3-4-5
5-12-13
6-8-10
7-24-25
8-15-17
9-12-15
9-40-41
10-24-26
11-60-61
12-16-20
12-35-37
13-84-85
14-48-50
15-20-25
15-36-39
15-112-113
16-30-34
16-63-65
17-144-145
18-24-30
18-80-82
19-180-181
20-21-29
20-48-52
20-99-101
21-28-35
21-72-75
21-220-221
22-120-122
23-264-265
24-32-40
24-45-51
24-70-74
24-143-145
25-60-65
25-312-313
26-168-170
27-36-45
27-120-123
27-364-365
28-45-53
28-96-100
28-195-197
29-420-421
30-40-50
30-72-78
30-224-226
31-480-481
32-60-68
32-126-130
32-255-257
33-44-55
33-56-65
33-180-183
33-544-545
34-288-290
35-84-91
35-120-125
35-612-613
36-48-60
36-77-85
36-105-111
36-160-164
36-323-325
37-684-685
38-360-362
39-52-65
39-252-255
39-760-761
40-42-58
40-75-85
40-96-104
40-198-202
40-399-401
41-840-841
42-56-70
42-144-150
42-440-442
43-924-925
44-117-125
44-240-244
44-483-485
45-60-75
45-108-117
45-200-205
45-336-339
46-528-530
48-55-73
48-64-80
48-90-102
48-140-148
48-189-195
48-286-290
48-575-577
49-168-175
50-120-130
50-624-626
51-68-85
51-140-149
51-432-435
52-165-173
52-336-340
52-675-677
54-72-90
54-240-246
54-728-730
55-132-143
55-300-305
56-90-106
56-104-119
56-192-200
56-390-394
56-783-785
57-76-95
57-176-185
57-540-543
58-840-842
59-540-549
60-63-87
60-80-100
60-91-109
60-144-156
60-175-185
60-297-303
60-448-452
60-899-901
62-960-962
63-84-105
63-216-225
63-280-287
63-660-663
64-120-126
64-252-260
64-510-514
65-72-97
65-156-169
65-420-429
66-88-110
66-112-130
66-360-366
68-285-293
68-576-580
69-92-115
69-260-269
69-792-795
70-168-182
70-240-250
72-96-120
72-135-153
72-154-170
72-210-222
72-320-328
72-429-435
72-646-650
75-100-125
75-180-195
75-308-317
75-560-565
75-936-939
76-357-365
76-720-724
77-264-275
77-420-427
78-104-130
78-160-178
78-504-510
80-84-116
80-150-170
80-192-208
80-315-325
80-396-404
81-108-135
81-360-369
84-112-140
84-135-159
84-187-205
84-245-259
84-288-300
84-437-445
84-585-591
84-880-884
85-132-157
85-204-221
85-720-725
87-116-145
87-416-425
88-105-137
88-165-187
88-234-250
88-480-488
88-966-970
90-120-150
90-216-234
90-400-410
90-672-678
91-312-325
91-588-595
92-525-533
93-124-155
93-476-485
95-168-193
95-228-247
95-900-905
96-110-146
96-128-160
96-180-204
96-247-265
96-280-296
96-378-390
96-572-580
96-765-771
98-336-350
99-132-165
99-168-195
99-440-451
99-540-549
100-105-145
100-248-260
100-495-505
100-621-629
102-136-170
102-280-298
102-864-870
104-153-185
104-195-221
104-330-346
104-672-680
105-140-175
105-do8-233
105-252-273
105-360-375
105-608-617
105-784-791
108-144-180
108-231-255
108-315-333
108-480-492
108-725-733
110-264-286
110-600-610
111-148-185
111-680-689
112-180-212
112-210-238
112-384-400
112-441-455
112-780-788
114-152-190
114-352-370
115-252-277
115-276-299
116-837-845
117-156-195
117-240-267
117-520-533
117-756-765
119-120-169
119-408-425
120-126-174
120-160-200
120-182-218
120-209-241
120-225-255
120-288-312
120-350-370
120-391-409
120-442-458
120-594-606
120-715-725
120-896-904
121-660-671
123-164-205
123-836-845
124-957-965
125-300-325
126-168-210
126-432-450
126-560-574
128-240-272
128-504-520
129-172-215
129-920-929
130-144-194
130-312-338
130-840-850
132-176-220
132-224-260
132-351-375
132-385-407
132-475-493
132-720-732
133-156-205
133-466-475
135-180-225
135-324-351
135-352-377
135-600-615
136-255-289
136-273-305
136-570-586
138-184-230
138-520-538
140-147-203
140-171-221
140-225-265
140-336-364
140-480-500
140-693-707
140-975-985
141-188-235
143-780-793
143-924-935
144-165-219
144-192-240
144-270-306
144-308-340
144-420-444
144-567-585
144-640-656
144-858-870
145-348-377
145-408-433
147-196-245
147-504-525
150-200-250
150-360-390
150-616-634
152-285-323
152-345-377
152-714-730
153-420-447
153-680-697
154-528-550
154-840-854
155-372-403
155-468-493
156-208-260
156-320-356
156-455-481
156-495-519
156-667-685
159-212-265
160-168-232
160-231-281
160-300-340
160-384-416
160-630-650
160-792-808
161-240-289
161-552-575
162-216-270
162-720-738
165-220-275
165-280-325
165-396-429
165-532-557
165-900-915
168-224-280
168-270-318
168-374-410
168-425-457
168-490-518
168-576-600
168-775-793
168-874-890
170-264-314
170-408-442
171-228-285
171-528-555
171-760-779
174-232-290
174-832-850
175-288-337
175-420-455
175-600-625
176-210-274
176-330-374
176-468-500
176-693-715
176-960-976
177-236-295
180-189-261
180-240-300
180-273-327
180-299-349
180-385-425
180-432-468
180-663-687
180-800-820
180-891-909
182-624-650
183-244-305
184-345-391
184-513-545
185-444-481
185-672-697
186-248-310
186-952-970
189-252-315
189-340-389
189-648-675
189-840-861
190-336-386
190-456-494
192-220.292
192-256-320
192-360-408
192-494-530
192-560-592
192-576-780
195-216-291
195-260-325
195-400-445
195-468-507
195-748-773
196-315-371
196-672-700
198-264-330
198-336-390
198-880-902
200-210-290
200-375-425
200-480-520
200-609-641
201-268-335
203-396-445
203-696-725
204-253-325
204-272-340
204-560-596
204-595-629
204-855-879
205-492-533
205-828-853
207-224-305
207-276-345
207-780-807
207-920-943
208-306-370
208-390-442
208-660-692
208-819-910
210-280-350
210-416-466
210-504-546
210-720-750
213-284-355
215-516-559
215-812-937
216-288-360
216-405-459
216-462-510
216-713-745
216-960-984
217-456-505
217-744-775
219-292-365
220-231-319
220-459-509
220-528-572
220-585-625
222-296-370
224-360-424
224-420-476
224-768-800
224-882-910
225-272-353
225-300-375
225-540-585
225-924-941
228-304-330
228-325-397
228-665-703
228-704-740
230-504-554
230-552-598
231-308-385
231-392-455
231-520-569
231-792-825
232-435-493
232-825-857
234-312-390
234-480-534
235-564-611
236-527-625
237-316-395
238-240-338
238-816-850
240-252-348
240-275-365
240-320-400
240-364-436
240-418-482
240-450-510
240-551-601
240-576-624
240-700-740
240-782-818
240-884-916
243-324-405
245-588-637
245-840-875
246-328-410
248-465-527
248-945-977
249-332-415
250-600-630
252-275-373
252-336-420
252-405-477
252-539-595
252-561-615
252-735-777
252-864-900
255-340-425
255-396-471
255-612-663
255-700-745
256-480-544
258-344-430
259-660-709
259-888-925
260-273-377
260-288-388
260-624-676
260-651-701
260-825-865
261-348-435
261-380-461
264-315-411
264-352-440
264-448-420
264-495-561
264-702-750
264-770-814
264-950-986
265-636-689
266-312-410
266-912-950
267-356-445
270-360-450
270-648-702
270-704-754
272-510-578
272-546-610
273-364-455
273-560-623
273-736-785
273-936-975
275-660-715
276-368-460
276-493-565
276-805-851
279-372-465
279-440-521
280-294-406
280-342-442
280-351-449
280-450-530
280-525-595
280-672-728
280-759-809
280-960-1000
282-376-470
285-380-475
285-504-579
285-684-741
285-880-925
287-716-865
288-330-438
288-384-480
288-540-612
288-616-680
288-741-795
288-840-888
290-696-754
290-816-866
291-388-485
294-392-490
295-708-767
296-555-629
300-315-435
300-400-500
300-455-545
300-589-661
300-720-780
300-875-925
301-900-949
303-404-505
304-570-646
304-650-754
305-732-793
306-408-510
306-840-894
308-435-533
308-495-583
308-819-875
309-412-415
310-744-806
310-936-986
312-416-520
312-459-555
312-585-663
312-640-712
315-420-525
315-572-653
315-624-600
315-756-819
318-424-530
319-360-481
320-336-464
320-462-562
320-600-680
321-428-535
322-480-578
324-432-540
324-693-765
324-945-999
325-360-485
325-780-845
327-436-545
328-615-697
330-440-550
330-560-650
330-792-858
332-495-657
333-444-555
333-644-725
335-804-871
336-377-505
336-385-511
336-448-560
336-540-636
336-630-714
336-748-820
336-850-914
339-452-565
340-528-628
340-357-493
340-816-884
341-420-541
342-456-570
344-645-731
345-460-575
345-756-831
345-828-897
348-464-580
348-805-877
350-576-674
350-840-910
351-468-585
352-420-548
352-660-748
352-936-1000
354-472-590
355-852-923
357-360-507
357-476-595
360-378-522
360-480-600
360-546-654
360-598-698
360-627-723
360-770-850
360-864-936
363-484-605
363-616-715
364-485-689
364-627-725
365-876-949
366-488-610
368-465-593
368-690-782
369-492-615
369-800-881
370-888-962
372-496-620
372-925-997
375-500-625
375-900-975
376-705-799
378-504-630
378-680-778
380-399-551
380-672-772
380-912-988
381-508-635
384-440-584
384-512-640
385-552-673
387-516-645
387-884-945
390-432-582
390-520-650
390-800-890
392-630-742
392-735-833
393-524-655
396-403-565
396-528-660
396-672-780
396-847-935
399-468-615
399-532-665
400-430-580
400-561-689
400-750-850
402-536-670
405-540-675
406-792-890
407-524-745
408-506-650
408-544-680
408-765-867
408-819-915
411-548-685
414-448-610
414-552-690
416-612-740
416-780-884
417-556-695
420-441-609
420-513-663
420-560-700
420-637-763
420-675-795
420-832-932
420-851-949
423-564-705
424-795-901
425-660-785
426-568-710
428-455-697
429-460-629
429-572-715
429-700-821
429-728-865
429-880-918
432-495-657
432-576-720
432-665-793
432-810-918
435-580-725
438-584-730
440-462-638
440-525-685
440-825-935
441-588-735
444-592-740
447-596-745
448-720-848
448-840-952
450-544-706
450-600-750
451-780-901
453-604-755
455-504-679
456-608-760
456-650-794
456-855-969
459-612-755
460-483-667
462-616-770
462-784-910
464-777-905
464-870-986
465-620-775
468-595-757
468-624-780
471-628-785
473-864-985
474-632-790
475-840-965
476-480-676
476-765-901
477-636-795
480-504-696
480-550-730
480-640-800
480-693-843
480-728-872
480-836-864
481-600-769
483-644-805
483-720-867
486-648-810
489-652-815
492-656-820
495-660-825
495-840-975
498-664-830
500-525-725
501-668-835
504-550-746
504-672-840
504-703-865
504-810-954
507-676-845
510-680-850
510-792-956
513-684-855
516-688-860
519-492-865
520-546-754
520-576-776
520-765-925
522-696-870
522-760-922
525-700-875
528-605-803
528-630-822
528-704-880
531-708-885
532-624-820
533-756-925
534-712-890
540-567-783
540-629-829
540-720-900
540-819-981
543-724-905
546-728-910
549-732-915
552-736-920
555-572-797
555-740-925
558-744-930
560-588-812
560-684-884
560-702-898
561-748-935
564-752-940
567-756-945
570-760-950
573-764-955
576-660-876
576-768-960
579-772-965
580-609-841
580-741-941
582-776-970
585-648-873
585-780-975
588-784-980
591-788-985
594-608-950
594-792-990
595-600-845
597-796-995
600-630-870
600-800-1000
612-759-975
615-728-953
616-663-905
616-735-959
620-651-899
621-672-915
624-715-949
640-672-928
650-720-970
660-693-957
680-714-986
696-697-985
Per trovare la
radice del quadrato di un numero compreso tra 11 e 99, si segue il procedimento
sotto riportato. Ma prima occorre sapere che, se il quadrato termina con 1, come
unit della radice si avr 1 o 9, se il quadrato termina con 4, come unit della
radice si avr 2 o 8; se il quadrato termina con 6, come unit della radice si
avr 4 o 6; se il quadrato termina con 5, come unit della radice si avr 5. Ma
ora passiamo a conoscere il procedimento.
1) si staccano
nel quadrato due cifre, da destra verso sinistra, che sarebbero poi le ultime
due, come appresso: 256 diventa 2'56; 1156 diventa 11'56.
2) si vede
qual il quadrato pi grande che contenuto nella parte di sinistra, nel
nostro caso in 2 e in 11. Cos conosceremo anche le decine della radice dei
quadrati in questione. Come possiamo renderci conto, 1 il quadrato pi grande
che contenuto nel 2, per cui la sua radice 1; mentre 9 il quadrato pi
grande che contenuto nell'11, per cui la sua radice 3.
3) siccome 256
termina con 6, come unit della radice si avr 4 o 6. Allora bisogner
moltiplicare la radice delle decine (1) per il suo successivo (2). Se il
prodotto contenuto nella prima parte del quadrato (2), si avr 6; se invece
non contenuto, si avr 4. Nel nostro caso, il 2 (1 2) contenuto nel 2, per
cui la radice delle unit sar 6. Quindi, avremo che la radice quadrata di 256
16.
Se
consideriamo 1156, terminando esso con 6, come unit della radice si avr 4 o 6.
Moltiplicando la radice delle decine (3) per il suo successivo (4), avremo come
prodotto 12. Siccome esso non contenuto nell'11, la radice delle unit sar 4.
Quindi, avremo che la radice quadrata di 1156 34.
Altri esempi:
Se il quadrato
121 (1'21), la radice delle decine (1) 1. Terminando esso con 1, la radice
delle unit 1 o 9. Siccome il 2 (1 2) non contenuto nell'1, la radice delle
unit 1. Quindi la radice quadrata di 121 11.
Se il quadrato
361 (3'61), la radice delle decine (3) 1. Terminando esso con 1, la radice
delle unit 1 o 9. Siccome 2 (1 2) contenuto nel 3, la radice delle unit
9. Quindi, la radice quadrata di 361 19.
Se il quadrato
324 (3'24), la radice delle decine (3) 1. Terminando esso con 4, la radice
delle unit 2 o 8. Siccome il 2 (1 2) contenuto nell'3, la radice delle
unit 8. Quindi la radice quadrata di 324 18.
Se il quadrato
144 (1'44), la radice delle decine (1) 1. Terminando esso con 4, la radice
delle unit 2 o 8. Siccome 2 (1 2) non contenuto nell'1, la radice delle
unit 2. Quindi, la radice quadrata di 144 12.
Se il quadrato
625 (6'25), la radice delle decine (6) 2. Terminando esso con 5, la radice
delle unit pu essere solo 5. Quindi, la radice quadrata di 625 25.
13) RADICE DEI CuBI DEI NuMERI DA 11 A 99
Per trovare la
radice del cubo di un numero compreso tra 11 e 99, si segue il procedimento
sotto riportato. Ma prima occorre sapere che: a) 1 il cubo di 1, 8 il cubo
di 2, 27 il cubo di 3, 64 il cubo di 4, 125 il cubo di 5, 216 il cubo di
6, 343 il cubo di 7, 512 il cubo di 8, 729 il cubo di 9; b) se il cubo
termina con 1, 9, 4, 6 e 5, tali cifre resteranno anche nelle unit delle
rispettive radici; se il cubo termina con 2, 8, 3 e 7, le unit delle rispettive
radici saranno i loro complementari. Ossia:
se il cubo
termina con 2, la radice delle unit sar 8; se invece termina con 8, la radice
delle unit sar 2. Se il cubo termina con 3, la radice delle unit sar 7, se
invece termina con 7, la radice delle unit sar 3.
Ma ora
passiamo a conoscere il procedimento.
1) si staccano
nel cubo tre cifre, da destra verso sinistra, che sarebbero poi le ultime tre,
come appresso: 19683 diventa 19'683; 79507 diventa 79'507.
2) si vede
qual il cubo pi grande che contenuto nella parte di sinistra, nel nostro
caso in 19 e in 79. Cos conosceremo anche le decine della radice dei cubi in
questione. Come possiamo renderci conto, 8 il cubo pi grande che contenuto
nel 19, per cui la sua radice 2; mentre 64 il cubo pi grande che
contenuto nell'11, per cui la sua radice 4.
3) Per
conoscere la radice delle unit , basta rifarsi a quanto detto sopra, ossia: se
il cubo termina con 1, 9, 4, 6 e 5, tali cifre resteranno anche nelle unit
delle rispettive radici; se il cubo termina con 2, 8, 3 e 7, le unit delle
rispettive radici saranno i loro complementari. Ossia:
se il cubo
termina con 2, la radice delle unit sar 8; se invece termina con 8, la radice
delle unit sar 2. Se il cubo termina con 3, la radice delle unit sar 7, se
invece termina con 7, la radice delle unit sar 3. Ma ora passiamo a conoscere
il procedimento.
Nel caso che
prendiamo in considerazione i cubi 19683 e 79507, le unit della radice cubica
del primo quadrato sono 7, per cui la sua radice cubica risulta 27; mentre le
unit della radice cubica del secondo cubo sono 3, per cui la sua radice cubica
diventa 43.
14) MOLTIPLICAZIONI DIRETTE MEDIANTE IL GRAFICO
Per eseguire
una moltiplicazione diretta bisogna memorizzare il grafico posto sulla sinistra
(il grafico si ottiene, unendo ogni estremo superiore di una linea con gli
estremi inferiori delle altre linee), tenendo presente: 1) ogni linea
rappresenta un prodotto dato dai due fattori posti ai suoi estremi; 2) ogni
pallino centrale indica un prodotto o la somma di due o pi prodotti, a seconda
delle linee che passano per esso; 3) alle somme centrali dei prodotti, come pure
al prodotto finale, va aggiunto l'eventuale riporto.
23
14
=
----------
322
Nella
moltiplicazione 23 14, avremo:
4 3
=12 (2 si scrive e 1 si riporta); 4 2 + 1 3 = 11 + 1 (riporto) = 12
(2 si scrive e 1 si riporta); 1 2 = 2 + 1 (riporto) = 3 (si scrive 3)
Risultato finale: 322
123
243
=
-------------
29.889
1234
2104 =
---------------
Nella
moltiplicazione 123 243, avremo:
3 3
= 9 (si scrive 9); 3 2 + 4 3 = 18 (8 si scrive e 1 si riporta); 3
1 + 2 3 + 4 2 = 17 + 1 (riporto) = 18 (8 si scrive e 1 si riporta);
4 1 + 2 2 = 8 + 1 (riporto) = 9 (si scrive 9); 2 1 = 2 (si scrive
2)
Risultato finale: 29.889
Nella
moltiplicazione 1234 2104, avremo:
4 4
= 16 (6 si scrive e 1 si riporta); 4 3 + 0 4 = 12 + 1 (riporto) = 13
(3 si scrive e 1 si riporta); 4 2 + 1 4 + 0 3 = 12 + 1 (riporto) =
13 (3 si scrive e 1 si riporta); 4 1 + 2 4 + 1 3 + 0 2 =15 + 1
(riporto) = 16 (6 si scrive e 1 si riporta); 2 3 + 0 1 + 1
2 = 8 + 1 (riporto) = 9 (si scrive 9); 1 1 + 2 2 = 5 (si scrive 5);
2 1 = 2 (si scrive 2)
Risultato finale: 2.596.336
15) MOLTIPLICAZIONI PER 11
5) TERNE PITAGORICHE
6) TERNE PITAGORICHE ENTRO IL 1000
B) ARITMETICA
7) COME OTTENERE I NuMERI PRIMI
I numeri primi si ottengono mediante due passaggi. Con il primo, avremo tutti i numeri primi contenuti in una certa quantit e i loro
multipli ottenuti con i loro quadrati e le loro moltiplicazioni con i numeri primi pi grandi. Con il secondo passaggio, ci sar
l eliminazione di tali prodotti, la quale ci permetter di avere soltanto i numeri primi.
PRIMO PASSAGGIO
Tale passaggio, come stato anticipato, ci far ottenere, nello stesso tempo, tutti i numeri primi e i loro multipli ottenuti come indicato, senza che li si possano distinguere. Gli uni e gli altri si avranno, eseguendo addizioni continue con gli operatori 4 e 2, avendo come partenza l unit , ossia 1. Via via vanno anche eliminati i multipli di 5.
Cos fino a 97, escluso il numero primo 3, avremo:
1+4=5+2=7+4=11+2=13+4=17+2=19+4=23+2=25+4=29+2=31+4=35+2=37+4=41+2=43+4=47+2=49+4=53+2=55+4=59+2=61+4=65+2=67+4=71+2=73+4=77+2=79+4=83+2=85+4=89+2=91+4=95+2=97.
Invece, da 97 a 200, avremo:
97+4=101+2=103+4=107+2=109+4=113+2=115+4=119+2=121+4=125+2=127+4=131+2=133+4=137+2=139+4=143+2=145+4=149+2=151+4=155+2=157+4=161+2=163+4=167+2=169+4=173+2=175+4=179+2=181+4=185+2=187+4=191+2=193+4=197+2=199.
SECONDO PASSAGGIO
Ottenuti i seguenti numeri, con l eliminazione dei multipli del 5:
5-7-11-13-17-19-23-29-31-37-41-43-47-49-53-59-61-67-71-73-77-79-83-89-91-97-101-103-107-109-113-119 -121 -127-131-133 -137-139 -143 -149-151-157-161 -163-167-169 -173-179-181-187 -191-193-197-199, si va alla ricerca dei numeri primi.
In tale serie di numeri, una volta eliminati i multipli del 7 (7x7=49, 7x11= 77, 7x13=91, 7x17=119, 7x19=133, 7x23=161), i multipli dell 11 (11x11=121, 11x13=143, 11x17=187), i multipli del 13 (13x13=169), restano solo i numeri primi.
Continuando con tale metodo, si ottiene la seguente prima tabella parziale, dove risultano i numeri primi (con il puntino accanto) e i loro multipli, come fatto presente:
2.
3.
7.
11.
13.
17.
19.
23.
29.
31.
37.
41.
43.
47.
49
53.
59.
61.
67.
71.
73.
77
79.
83.
89.
91
97.
101.
103.
107.
109.
113.
119
121
127.
131.
133
137.
139.
143
149.
151.
157.
161
163.
167.
169
173.
179.
181.
187
191.
193.
197.
199.
203
209
211.
217
221
223.
227.
229.
233.
239.
241.
247
251.
253
257.
259
263.
269.
271.
277.
281.
283.
287
289
293.
299
301
307.
311.
313.
317.
319
323
329
331.
337.
341
343
347.
349.
353.
359.
361
367.
371
373.
377
379.
383.
389.
391
397.
401.
403
407
409.
413
419.
421.
427
431.
433.
437
439.
443.
449.
451
457.
461.
463.
467.
469
473
479.
481
487.
491.
493
497
499.
503.
509.
511
517
521.
523.
527
529
533
539
541.
547.
551
553
557.
559
563.
569.
571.
577.
581
583
587.
589
593.
599.
601.
607.
611
613.
617.
619.
623
629
631.
637
641.
643.
647.
649
653.
659.
661.
667
671
673.
677.
679
683.
701.
703
707
709.
713
719.
721
727.
731
733.
737
739.
743.
749
751.
757.
761.
763
767
769.
773.
779
781
787.
791
793
797.
799
689
691.
697
803
809.
811.
817
821.
823.
827.
829.
833
839.
841
847
851
853.
857.
859.
863.
869
871
877.
881.
883.
887.
889
893
899
901
907.
911.
913
917
919.
923
929.
931
937.
941.
943
947.
949
953.
959
961
967.
971.
973
977.
979
983.
989
991.
997.
1001
1003
1007
1009.
1013.
1019.
1021.
1027
1031.
1033.
1037
1039.
1043
1049.
1051.
1057
1061.
1063.
1067
1069.
1073
1079
1081
1087.
1091.
1093.
1097.
1099
1103.
1109.
1111
1117.
1121
1123.
1127
1129.
1133
1139
1141
1147
1151.
1153.
1157
1159
1163.
1169
1171.
1177
1181.
1183
1187.
1189
1193.
1199
1201.
1207
1211
1213.
1217.
1219
1223.
1229.
1231.
1237.
1241
1243
1247
1249.
1253
1259.
1261
1267
1271
1273
1277.
1279.
1283.
1289.
1291.
1297.
1301.
1303.
1307.
1309
1313
1319.
1321.
1327.
1331
1333
1337
1339
1343
1349
1351
1357
1361.
1363
1367.
1369
1373.
1379
1381.
1387
1391
1393
1397
1399.
1403
1409.
1411
1417
1421
1423.
1427.
1429.
1433.
1439.
1441
1447.
1451.
1453.
1457
1459.
1463
1469
1471.
1477
1481.
1483.
1487.
1489.
1493.
1499.
1501
1507
1511.
1513
1517
1519
1523.
1529
1531.
1537
1541
1543.
1547
1549.
1553.
1559.
1561
1567.
1571.
1573
1577
1579.
1583.
1589
1591
1597.
1601.
1603
1607.
1609.
1613.
1619.
1621.
1627.
1631
1633
1637.
1639
1643
1649
1651
1657.
1661
1663.
1667.
1669.
1673
1679
1681
1687
1691
1693.
1697.
1699.
1703
1709.
1711
1717
1721.
1723.
1727
1729
1733.
1739
1741.
1747.
1751
1753.
1757
1759.
1763
1769
1771
1777.
1781
1783.
1787.
1789.
1793
1799
1801.
1807
1811.
1813
1817
1819
1823.
1829
1831.
1837
1841
1843
1847.
1849
1853
1859
1861.
1867.
1871.
1873.
1877.
1879.
1883
1889.
1891
1897
1901.
1903
1907.
1909
1913.
1919
1921
1927
1931.
1933.
1937
1939
1943
1949.
1951.
1957
1961
1963
1967
1969
1973.
1979.
1981
1987.
1991
1993
1997.
1999.
2003.
2009
2011.
2017.
2021
2023
2027.
2029.
2033
2039.
2041
2047
2051
2053.
2057
2059
2063.
2069.
2071
2077
2081.
2083.
2087.
2089.
2093
2099.
2101
2107
2111.
2113.
2117
2119
2123
2129.
2131.
2137.
2141.
2143.
2147
2149
2153.
2159
2161.
2167
2171
2173
2177
2179.
2183
2189
2191
2197
2201
2203.
2207.
2209
2213.
2219
2221.
2227
2231
2233
2237.
2239.
2243.
2249
2251.
2257
2261
2263
2267.
2269.
2273.
2279
2281.
2287.
2291
2293.
2297.
2299
2303
2309
2311.
2317
2321
2323
2327
2329
2333.
2339.
2341.
2347.
2351.
2353
2357.
2359
2363
2369
2371.
2377.
2381.
2383.
2387
2389.
2393.
2399.
2401
2407
2411.
2413
2417.
2419
2423.
2429
2431
2437.
2441.
2443
2447.
2449
2453
2459.
2461
2467
2471
2473.
2477.
2479
2483
2489
2491
2497
2501
2503.
2507
2509
2513
2519
2521.
2527
2531.
2533
2537
2539.
2543.
2549.
2551.
2557.
2561
2563
2567
2569
2573
2579.
2581
2587
2591.
2593.
2597
2599
2603
2609.
2611
2617.
2621.
2623
2627
2629
2633.
2639
2641
2647.
2651
2653
2657.
2659.
2663.
2669
2671.
2677.
2681
2683.
2687.
2689.
2693.
2699.
2701
2707.
2711.
2713.
2717
2719.
2723
2729.
2731.
2737
2741.
2743
2747
2749.
2753.
2759
2761
2767.
2771
2773
2777.
2779
2783
2789.
2791.
2797.
2801.
2803.
2807
2809
2813
2819.
2821
2827
2831
2833.
2837.
2839
2843.
2849
2851.
2857.
2861.
2863
2867
2869
2873
2879.
2881
2887.
2891
2893
2897.
2899
2903.
2909.
2911
2917.
2921
2923
2927.
2929
2933
2939.
2941
2947
2951
2953.
2957.
2959
2963.
2969.
2971.
2977
2981
2983
2987
2989
2993
2999.
3001.
3007
3011.
3013
3017
3019.
3023.
3029
3031
3037.
3041.
3043
3047
3049.
3053
3059
3061.
3067.
3071
3073
3077
3079.
3083.
3089.
3091
3097
3101
3103
3107
3109.
3113
3119.
3121.
3127
3131
3133
3137.
3139
3143
3149
3151
3157
3161
3163.
3167.
3169.
3173
3179
3181.
3187.
3191.
3193
3197
3199
3203.
3209.
3211
3217.
3221.
3223
3227
3229.
3233
3239
3241
3247
3251.
3253.
3257.
3259.
3263
3269
3271.
3277
3281
3283
3287
3289
3293
3299.
3301.
3307.
3311
3313.
3317
3319.
3323.
3329.
3331.
3337
3341
3343.
3347.
3349
3353
3359.
3361.
3367
3371.
3373.
3377
3379
3383
3389.
3391.
3397
3401
3403
3407.
3409
3413.
3419
3421
3427
3431
3433.
3437
3439
3443
3449.
3451
3457.
3461.
3463.
3467.
3469.
3473
3479
3481
3487
3491.
3493
3497
3499.
3503
3509
3511.
3517.
3521
3523
3527.
3529.
3533.
3539.
3541.
3547.
3551
3553
3557.
3559.
3563
3569
3571.
3577
3581
3583.
3587
3589
3593.
3599
3601
3607.
3611
3613.
3617.
3619
3623.
3629
3631.
3637.
3641
3643.
3647
3649
3653
3659.
3661
3667
3671.
3673.
3677.
3679
3683
3689
3691.
3697.
3701.
3703
3707
3709.
3713
3719.
3721
3727.
3731
3733.
3737
3739.
3743
3749
3751
3757
3761.
3763
3767.
3769.
3773
3779.
3781
3787
3791
3793.
3797.
3799
3803.
3809
3811
3817
3821.
3823.
3827
3829
3833.
3839
3841
3847.
3851.
3853.
3857
3859
3863.
3869
3871
3877.
3881.
3883
3887
3889.
3893
3899
3901
3907.
3911.
3913
3917.
3919.
3923.
3929.
3931.
3937
3941
3943.
3947.
3949
3953
3959
3961
3967.
3971
3973
3977
3979
3983
3989.
3991
3997
4001.
4003.
4007.
4009
4013.
4019.
4021.
4027.
4031
4033
4037
4039
4043
4049.
4051.
4057.
4061
4063
4067
4069
4073.
4079.
4081
4087
4091.
4093.
4097
4099.
4103
4109
4111.
4117
4121
4123
4127.
4129.
4133.
4139.
4141
4147
4151
4153.
4157.
4159.
4163
4169
4171
4177.
4181
4183
4187
4189
4193
4199
4201
4207
4211
4213
4217.
4219.
4223
4229.
4231.
4237
4241.
4243.
4247
4249
4253.
4259.
4261
4267
4271.
4273.
4277
4279
4283.
4289.
4291
4297.
4301
4303
4307
4309
4313
4319
4321
4327.
4331
4333
4337.
4339.
4343
4349.
4351
4357.
4361
4363.
4367
4369
4373.
4379
4381
4387
4391.
4393
4397.
4399
4403
4409.
4411
4417
4421.
4423.
4427
4429
4433
4439
4441.
4447.
4451.
4453
4457.
4459
4463.
4469
4471
4477
4481.
4483.
4487
4489
4493.
4499
4501
4507.
4511
4513.
4517.
4519.
4523.
4529
4531
4537
4541
4543
4547.
4549.
4553
4559
4561.
4567.
4571
4573
4577
4579
4583.
4589
4591.
4597.
4601
4603.
4607
4609
4613
4619
4621.
4627
4631
4633
4637.
4639.
4643.
4649.
4651.
4657.
4661
4663.
4667
4669
4673.
4679.
4681
4687
4691.
4693
4697
4699
4703.
4709
4711
4717
4721.
4723.
4727
4729.
4733.
4739
4741
4747
4751.
4753
4757
4759.
4763
4769
4771
4777
4781
4783.
4787.
4789.
4793.
4799.
8) DAI MuLTIPLI DEL 6 AI NuMERI PRIMI
a) un numero primo risulta sempre un multiplo di 6, a cui stata aggiunta o sottratta l unit . Esso pu (ma non obbligatoriamente) derivare dalla sottrazione o dall aggiunta dell unit , oppure da entrambe le operazioni. In quest ultimo caso, i due numeri primi ottenuti sono detti gemelli. Ne deriva che un numero dispari, che non termina con 5, pu essere primo, se risulta un multiplo di 6, dopo aver aggiunto o sottratto ad esso l unit , oppure in entrambi i casi.
Ad esempio, se prendiamo 24, che un multiplo di 6, esso ci d un numero primo, solo se sottraiamo ad esso l unit , ottenendo 23. Se invece aggiungiamo ad esso l unit , otteniamo il numero composto 25.
Se invece prendiamo 18, che anche un multiplo di 6, aggiungendo e sottraendo ad esso l unit , otteniamo rispettivamente i due numeri primi 17 e 19, che sono detti gemelli. Infatti, due numeri primi aventi per differenza 2 prendono il nome di gemelli.
I multipli del 6, nei loro rapporti con i numeri primi, risultano di quattro tipi:
1) Multipli che non danno alcun numero primo, sia che si aggiunga ad essi l'unit sia che si sottragga dagli stessi l unit :
120-1=119; 120+1=121. (119 e 121 non sono numeri primi).
2) Multipli che danno un numero primo, solo se si aggiunge ad essi l unit :
36+1=37 (37 numero primo).
3) Multipli che danno un numero primo, solo se si sottrae ad essi l unit :
54-1=53 (53 numero primo).
4) Multipli che danno un numero primo, sia che si aggiunga sia che si sottragga ad essi l unit :
132+1=133; 132-1=131 (133 e 131 sono numeri primi)
Ci sono pure tre tipi di coppie di numeri primi gemelli:
1) Coppia, nella quale il numero primo minore termina con 1 e il maggiore termina con 3, come le seguenti:
11-13; 41-43; 71-73; 101-103; 191-193; 281-283.
2) Coppia, nella quale il numero primo minore termina con 7 e il minore termina con 9, come le seguenti:
17-19; 107-109; 137-139; 197-199; 227-229; 347-349.
3) Coppia, nella quale il numero primo minore termina con 9 e il minore termina con 1, come le seguenti:
29-31; 59-61; 149-151; 239-241; 269-271; 599-601.
Risulta divisibile per 6 anche la somma di due numeri primi ottenuti l uno con +1 e l altro con -1.
73 (72+1) + 107 (108-1) = 180 (divisibile per 6).
Se due numeri primi sono stati ottenuti entrambi con +1, sottraendo alla loro somma due unit , si ottiene un numero divisibile per 6.
151 (150+1) + 277 (276+1) = 428 - 2 = 426 (divisibile per 6).
Se due numeri primi sono stati ottenuti entrambi con -1, aggiungendo alla loro somma due unit , si ottiene un numero divisibile per 6.
269 (270-1) + 605 (606-1) = 874 + 2 = 876 (divisibile per 6)
b) Se un quadrato divisibile solo per s stesso e per la sua radice, quest ultima un numero primo.
49 divisibile solo per s stesso e per 7, che la sua radice. Per cui 7 un numero primo.
Allora vero anche che il quadrato di un numero primo il suo primo multiplo avente come fattori la sua radice.
Il quadrato di 7 49, i cui fattori sono 7x7.
c) Se dividiamo un numero primo per 6, avremo come resto 1 oppure 5, a seconda se stata aggiunta oppure tolta l unit .
31 : 6 = 5 col resto di 1 (Infatti al multiplo 30 stata sommata l unit , facendolo diventare 31, che un numero primo).
29 : 6 = 4 col resto di 5 (Infatti, al multiplo 30 stata sottratta l unit , facendolo diventare 29, che un numero primo).
d) un numero primo anche la somma di un multiplo di 6 pi un numero primo pi piccolo di quello che si vuole ottenere. Quando il multiplo di 6 termina con 0, ad esso non si pu sommare il numero primo 5, poich ne verrebbe fuori un multiplo di 5. A volte lo stesso multiplo di 6, con i vari numeri primi aggiunti, d luogo ad altrettanti numeri primi. Come pure due addendi diversi, sommati, possono dare lo stesso numero primo.
6 + 11 = 17 (11 e 17 sono numeri primi);
12 + 5 = 17 (5 e 17 sono numeri primi);
6 + 23 = 29 (23 e 29 sono numeri primi);
12 + 19 = 31 (19 e 31 sono numeri primi);
18 + 19 = 37 (19 e 37 sono numeri primi);
42 + 59 = 101 (59 e 101 sono numeri primi); ecc
e) Se si vuole sapere quale multiplo di 6 ha dato origine al numero primo, bisogna prima renderlo multiplo di 6 (aggiungendo o sottraendo ad esso l unit ), come di seguito:
Se abbiamo il numero primo 56443 e vogliamo conoscere il multiplo di 6 che gli ha dato origine, prima eseguiamo le due operazioni e sommiamo le cifre dei due risultati [56443+1=56444 (23)], [56443-1=56442 (21)]. Essendo 21 divisibile per 3, 56442 risulta divisibile per 6. Per cui il multiplo di 6 che ha dato origine al numero primo 56443 56442.
Nel caso di due numeri primi gemelli, come 34757 e 34759, il multiplo di 6, che ha dato origine ad entrambi, il loro numero intermedio, ossia 34758.
Se la somma di due numeri primi divisibile per 6, l uno stato ottenuto da un multiplo di 6 a cui stata tolta l unit e l altro stato ottenuto da un multiplo di 6 a cui stata aggiunta l unit , come nei seguenti:
317 + 643 = 960 : 6 = 160 (318-1 = 317 / 642+1 = 643)
Nei numeri primi gemelli avviene la stessa cosa. Essi per sono stati ottenuti dallo stesso multiplo di 6.
f) Ogni numero primo ha infiniti multipli, i quali si possono dividere in due gruppi: a) quelli ottenuti dal suo prodotto con numeri non primi, come 9, 10, 12, che sono infiniti; b) quelli ottenuti dal suo prodotto con numeri primi, come 11, 13, 17, che sono pure infiniti. Questo secondo gruppo d origine a dei prodotti aventi per fattori due numeri primi. Cos 91, che un multiplo di 7, ha per fattori 7 e 13. un multiplo di questo tipo possiamo considerarlo multiplo bifattoriale primo; invece 12, che un multiplo di 3 ed ha per fattori 3 e 4, da considerarsi un multiplo bifattoriale non primo. Se nel primo caso il multiplo 91 pu avere una sola coppia di fattori, cio 7 e 13; nel secondo caso, il multiplo 12 pu avere due coppie di fattori, ossia 3 e 4, 2 e 6.
h) I numeri primi terminano sempre con le cifre 1, 3, 7 e 9. Ora vediamo come si ottengono i numeri primi terminanti con tali cifre.
1)I multipli del 6 ottenuti con i numeri terminanti con 2 e con 7 possono diventare numeri primi, sottraendo ad essi una unit . Tali numeri primi terminano tutti con la cifra 1. Esempi:
6 x 32 = 192 1 = 191; 6 x 47 = 282 1 = 281 (191 e 281 sono numeri primi).
Anche i multipli del 6 ottenuti con un multiplo del 5 e aumentati di una unit danno luogo a numeri primi terminanti con 1. Esempi:
6 x 5 = 30 + 1 = 31 / 6 x 30 = 180 + 1 = 181 (31 e 181 sono numeri primi)
Comunque, per avere i numeri primi in ordine crescente, bisogna procedere alternativamente prima con il 2, poi con il 5 e infine con il 7.
2 x 6 = 12 1 = 11 / 5 x 6 = 30 + 1 = 31 / 7x6=42-1=41 (Infatti, i numeri 11, 31 e 41 sono tre numeri primi in ordine crescente).
2) I multipli del 6 ottenuti con i numeri terminanti con 4 e con 9 possono diventare numeri primi, sottraendo ad essi l unit . I numeri primi ottenuti con tale criterio terminano tutti con la cifra 3. Esempi:
6 x 14 = 84 1 = 83 / 6 x 29 = 174 1 = 173
Anche i multipli del 6 ottenuti con i numeri terminanti con 2 e con 7 possono diventare numeri primi, aggiungendo ad essi l unit . Anch essi terminano tutti con la cifra 3. Esempi:
12 x 6 = 72 + 1 = 73 / 17 x 6 = 102 + 1 = 103 (73 e 103 sono numeri primi)
3) I multipli del 6 ottenuti con i numeri terminanti con 1 e con 6 possono diventare numeri primi, aggiungendo ad essi l unit . Tali numeri primi terminano con la cifra 7. Esempi:
6 x 6 = 36 + 1 = 37 / 6 x 11 = 66 + 1 = 67 (37 e 67 sono numeri primi)
Anche i multipli del 6 ottenuti con numeri terminanti con 3 e con 8 possono diventare numeri primi, sottraendo ad essi l unit . Anch essi terminano con la cifra 7. Esempi:
6 x 23 = 138 1 = 137; 6 x 58 = 348 1=347 (Anche i numeri primi ottenuti con tale criterio terminano tutti con la cifra 7)
4) I multipli del 6 ottenuti con i numeri terminanti con 3 e con 8 possono diventare numeri primi, aggiungendo ad essi l unit . I numeri primi ottenuti con tale criterio terminano tutti con la cifra 9. Esempi:
6 x 13 = 78 + 1 = 79 / 6 x 38 = 228 + 1 = 229 (79 e 229 sono numeri primi)
Anche i multipli del 6 ottenuti con i multipli del 5, diminuiti di una unit , possono diventare numeri primi. Anch essi terminano tutti con la cifra 9. Esempi:
5 x 6 = 30 1 = 29; 30 x 6 = 180 1 = 179 (29 e 179 sono numeri primi)
9) SuI QuADRATI DEI NuMERI INTERI
Esiste una correlazione tra i quadrati in successione e i numeri dispari, la quale è la seguente: partendo da 0, tutti i quadrati successivi si ottengono, aggiungendo ad esso i vari numeri dispari in successione.
Il quadrato di un numero n è uguale alla somma dei primi n numeri dispari. Ossia:
3² = 1+3+5=9;
5² = 1+3+5+7+9=25;
9² = 1+3+5+7+9+11+13+15+17=81.
Se bisogna trovare i quadrati di più numeri consecutivi, basta aggiungere ogni volta al quadrato precedente la loro somma, come qui appresso.
Volendo trovare i quadrati dei numeri da 1 a 10, abbiamo:
1² = 1;
2² =1 + 3 (2 + 1) = 4;
3² = 4 + 5 (2 + 3) = 9;
4² = 9 + 7 (3 + 4) = 16;
5² = 16 + 9 (4 + 5) = 25; ecc.
- Conoscendosi n e il suo quadrato, è semplice conoscere qual è stato il numero dispari più grande della serie di numeri dispari, la cui somma ha dato luogo al quadrato. Infatti, esso si ottiene, moltiplicando n per 2 e sottraendo al prodotto 1.
Se sappiamo che il quadrato di 40 è 1600, sappiamo anche che è stata la somma dei primi 40 numeri dispari a dar luogo a 1600, il più grande dei quali è stato: 40 x 2 - 1 = 79. Per cui, se volessimo trovare il quadrato di 41, basterebbe aggiungere a 1600 il successivo numero dispari, che è 81, (1600 + 81 = 1681). Se invece volessimo trovare il quadrato di 39, basterebbe sottrarre da 1600 il numero dispari più grande, che è 79, (1600 - 79 = 1521).
- Da ciò possiamo dedurre che, tutte le volte che dobbiamo trovare il quadrato dei numeri come 51 e 49, ci conviene trovare prima il quadrato di 50 (2500). Dopo aggiungiamo 101 (2601) per trovare il quadrato di 51 o sottraiamo 99 (2401) per trovare il quadrato di 49.
- Se vogliamo trovare i quadrati di tutti i numeri dispari, a partire dal quadrato 1, basta aggiungere ad esso di seguito 8 e i suoi multipli, come appresso:
1² + 8 = 9 (quadrato di 3) + 16 = 25 (quadrato di 5) + 24 = 49 (quadrato di 7) + 32 = 81 (quadrato di 9) + 40 = 121 (quadrato di 11) + 48 = 169 (quadrato di 13); ecc.
- Se vogliamo trovare i quadrati di tutti i numeri pari, a partire dal quadrato di 2, ossia 4, basta aggiungere ad esso di seguito 8 e i suoi multipli aumentati di 4, come appresso:
4 (quadrato di 2) + 12 (8 + 4) = 16 (quadrato di 4) + 20 (16 + 4) = 36 (quadrato di 6) + 28 (24 + 4) = 64 (quadrato di 8) + 36 (32 + 4) = 100 (quadrato di 10) + 44 (40 + 4) = 144 (quadrato di 12) + 52 (48 + 4) = 196 (quadrato di 14); ecc.
b) Esiste anche una formula per trovare il quadrato di un numero di due cifre, alla quale, senza eseguire la moltiplicazione, possiamo ricorrere, tutte le volte che troviamo la convenienza.
Se a e b sono rispettivamente le decine e le unità del numero, abbiamo la seguente formula aritmetica:
n² = a² + 2ab + b²
Così, dovendo trovare il quadrato di 56, applicando la formula, avremo:
56² =(50² = 2500) + (50 x 6 x 2 = 600) + (6² = 36) = 2500 + 600 + 36 = 3136
Esiste anche una formula per trovare il quadrato di un numero di tre cifre, alla quale, senza eseguire la moltiplicazione, possiamo ricorrere, tutte le volte che troviamo la convenienza.
Se a, b e c sono rispettivamente le centinaia, le decine e le unità del numero, abbiamo la seguente formula aritmetica:
n² = (a²) + (2ab) + (2ac) + (b²) + (2bc) + c²
Così, dovendo trovare il quadrato di 125, applicando la formula, avremo:
125² = (100² = 10000) + (100 x 20 x 2 = 4000); + (100 x 5 x 2 = 1000) + (20² = 400) + (20 x 5 x 2 = 200) + (5² = 25) = 10.000 + 4000 + 1000 + 400 + 200 + 25 = 15.625
c) Se si conoscono il prodotto di due numeri ab (a il maggiore e b il minore), i loro quadrati a² e b², la loro differenza (a-b) oppure la loro somma (a+b), si hanno come formule:
- la loro somma à data dalla differenza dei loro quadrati diviso la loro differenza: a + b = (a² - b²) : (a-b);
- la loro differenza è data dalla differenza dei loro quadrati diviso la loro somma: a - b = (a² - b²) : (a + b);
- il numero maggiore à dato dalla differenza tra il suo quadrato e il loro prodotto diviso la loro differenza: a = a² - ab : (a - b);
- il numero minore è dato dalla differenza tra il loro prodotto e il suo quadrato diviso la loro differenza: b = ab - b² : (a - b).
In pratica, avremo:
Se il prodotto dei due numeri consecutivi a e b è 12 e i loro rispettivi quadrati sono 16 e 9, nonché si conosce la loro differenza 1 oppure la loro somma 7, applicando le formule, avremo:
a + b = (a² - b²) : (a - b) = (16 - 9) : 1 = 7 : 1 = 7;
a b = (a² - b²) : (a - b) = (16 - 9) : 7 = 7 : 7 = 1;
a = a² - ab : (a - b) = 16 - 12 = 4;
b = ab - b² : (a - b) = (12 - 9) : 1 = 3 : 1 = 3
Inoltre, il prodotto dei due numeri è medio proporzionale tra i due quadrati: a² : ab = ab : b².
Perciò avremo:16 : 12 = 12 : 9.
Se la differenza fra due numeri consecutivi è sempre 1, la differenza fra i loro quadrati è la loro somma. Prendendo ad esempio la coppia di numeri 6 e 5, la loro differenza è 1 (6 - 5 = 1); mentre la differenza dei loro quadrati è 11 (6 + 5 = 11). Infatti, 36 - 25 = 11.
10) SuI CuBI DEI NuMERI INTERI
Anche i cubi dei numeri, come i quadrati, sono dati dalla somma di più numeri dispari, ma in modo diverso. Infatti, ciascuno si ottiene come segue:
1) Procedimento con i numeri interi dispari
Volendo conoscere il cubo di 3, esso ù dato da tre numeri dispari consecutivi, che si ottengono nel modo seguente: il primo è il quadrato di 3, ossia 9; gli altri due sono 7 (il precedente) e 11, (il successivo). Perciò avremo: 3³=7+9+11=27.
Volendo conoscere il cubo di 5, esso dato da cinque numeri dispari consecutivi, che si ottengono nel modo seguente: il primo il quadrato di 5, ossia 25; gli altri quattro sono 21 e 23 (i precedenti), nonché 27 e 29 (i successivi). Perciò avremo: 5³=21+23+25+27+29=125.
1) Procedimento con i numeri interi pari
Volendo conoscere il cubo di 2, esso è dato da due numeri dispari consecutivi, che si ottengono nel modo seguente: il primo è il precedente del quadrato di 2 (che è 4), ossia 3; il secondo è il successivo del quadrato di 2, che è 5. Perciò avremo: 2³=3+5=8
Volendo conoscere il cubo di 4, esso è dato da quattro numeri dispari consecutivi, che si ottengono nel modo seguente: i primi due sono i precedenti del quadrato di 4 (che è 16), ossia 13 e 15; mente gli altri due sono i successivi del quadrato di 4, ossia 17 e 19. Perciò avremo: 4³=13+15+17+19=64
11) IL MEDIANO E I SuOI SIMMETRICI
Dato un numero n, che chiameremo mediano, le coppie di numeri formati con l aggiunta e la sottrazione di 1, oppure di 2, ecc sono detti suoi simmetrici. Perci i simmetrici di 7 sono 7 + 1 = 8 e 7 1 = 6. Dei due simmetrici, il primo detto maggiore e il secondo detto minore. Le coppie di simmetrici di un mediano non sono illimitate, poich il loro numero uguale al mediano diminuito di una unit . Ossia, se il mediano 15, le coppie di simmetrici ad esso appartenenti sono in tutto 14, ossia 14 e 16, 13 e 17, 12 e 18, 11 e 19, ecc...
Adesso possiamo dire che il quadrato di un mediano dato anche dalla somma del prodotto dei suoi simmetrici pi il quadrato della loro semidifferenza. Perci avremo:
42 = 5 3 + 12 = 15 + 1 = 16 (Qui i simmetrici sono stati ottenuti con +1 e -1)
72= 9 5 + 22 = 45 + 4 = 49 (Qui i simmetrici sono stati ottenuti con +2 e -2)
Se si conoscono due numeri simmetrici, il loro mediano uguale alla loro semisomma. Perci , se abbiamo i simmetrici 10 e 8, il loro mediano :
(10 + 8) : 2 = 18 : 2 = 9
In geometria, se il mediano rappresenta il lato di un quadrato, i suoi simmetrici rappresentano le dimensioni di un rettangolo. In tal caso, diciamo che il quadrato e il rettangolo sono in relazione fra loro. Per cui, se un quadrato e un rettangolo sono in relazione fra loro, il lato del quadrato va considerato mediano e le dimensioni del rettangolo vanno considerate suoi simmetrici. La qual cosa pu facilitarci la soluzione di alcuni problemi geometrici.
un quadrato e un rettangolo, che ha per dimesioni cm 7 e cm 9, sono in relazione fra loro. Trovare l area del quadrato.
Essendo 7 e 9 simmetrici, il loro mediano il lato del quadrato. Perci :
(7 + 9) : 2 = 16 : 2 = cm 8; da cui:
A = 82 = cm2 64
un rettangolo e un quadrato, che ha per lato cm 13, sono in relazione fra loro. Trovare l area del rettangolo, la cui dimensione minore misura cm 11.
Se 13 il mediano e 11 il simmetrico minore, la dimensione maggiore del rettangolo cm 15. Allora l area del rettangolo sar uguale a:
A = 15 11 = cm2 165
12) RADICE DEI QuADRATI DEI NuMERI DA 11 A 99



2.596.336
Numeri con due cifre
19) Nomi dei Multipli e dei Sottomultipli delle Potenze del 10
Il prodotto di un numero di due cifre per 11 si ottiene in questo modo: a destra si pone la cifra delle unit del numero e a sinistra si pone il numero stesso aumentato della cifra indicante le sue decine.
Se dobbiamo moltiplicare 36x11, scriviamo a destra 6 e a sinistra 39 (36+3). Quindi il risultato finale sar 396.
Se dobbiamo moltiplicare 17x11, scriviamo a destra 7 e a sinistra 18 (17+1). Quindi il risultato finale sar 187.
Se dobbiamo moltiplicare 36x11, scriviamo a destra 6 e a sinistra 39 (36+3). Quindi il risultato finale sar 396.
Se dobbiamo moltiplicare 92x11, scriviamo a destra 2 e a sinistra 101 (92+9). Quindi il risultato finale sar 1012.
Numeri con tre cifre
Il prodotto di un numero di tre cifre per 11 si ottiene in questo modo: a destra si pone la cifra delle unit del numero e a sinistra si pone il numero stesso aumentato del numero formato dalle sue due prime cifre.
Se dobbiamo moltiplicare 123x11, scriviamo a destra 3 e a sinistra 135 (123+13). Quindi il risultato finale sar 1353.
Se dobbiamo moltiplicare 925x11, scriviamo a destra 5 e a sinistra 1017 (925+92). Quindi il risultato finale sar 10175.
Allo stesso modo si pu procedere anche con numeri che hanno pi di tre cifre.
16) NuOVO SISTEMA NuMERICO IN LETTERE
Prima di andare avanti nell'apprendimento del nuovo sistema numerico in lettere, utile venire a conoscenza della pronuncia delle consonanti usate per formare i numeri. Al riguardo, va fatto presente:
Le vocali E ed O hanno sempre suono aperto, come in setta e in posta;
Le consonanti C e G hanno suono dolce anche davanti ad A, O e u. Il loro suono duro dato rispettivamente dalle consonanti K e H. Perci ha si legge ga e he si legge ghe.
La consonante X ha il suono del sc dolce italiano. Quindi, xa si legge sci e xe si legge sce.
Le consonanti B, D, F, L, M, N, P, R, S, T, V, Z si leggono come nella lingua italiana.
17) I Numeri: dalle unit ai Miliardi
In lettere, i numeri da 0 a 9 sono i seguenti:
Voev=zero; bir=uno; fic=due; kid=tre; lig=quattro; mih=cinque; pin=sei; riv=sette; six=otto; tiz=nove.
I restanti numeri, sempre in lettere, si formano mediante le seguenti regole:
1) Le decine si ottengono, frapponendo una a tra la consonante iniziale e la vocale i delle unit . L accento cade sulla vocale a.
bair=dieci; faic=venti; kaid=trenta; laig=quaranta; maih=cinquanta;
pain=sessanta; raiv=settanta; saix=ottanta; taiz=novanta.
2) Le centinaia si ottengono, frapponendo una e fra la vocale i e la consonante finale delle unit . L accento cade sulla vocale i.
bier=cento; fiec=duecento; kied=trecento; lieg=quattrocento;
mieh=cinquecento; pien=seicento; riev=settecento;
siex=ottocento; tiez=novecento.
3) I numeri formati da decine e unit si ottengono, aggiungendo le unit alle decine e privando queste ultime della loro consonante finale.
Baitiz=diciannove; laimih=quarantacinque; paisix=sessantotto; taibir=novantuno; fairiv=ventisette; maipin=sessantasei; kaific=trentadue; rairiv=settantasette.
4) I numeri formati da centinaia e unit si ottengono, aggiungendo le unit alle centinaia e privando queste ultime della loro consonante finale.
Biebir=centouno; fiekid=duecentotre; lietiz=quattrocentonove; miesix=cinquecentootto; piemih=seicentocinque; rielig=settecentoquattro; kiekid=trecentotre.
5) I numeri formati da centinaia e decine si ottengono, aggiungendo le decine alle centinaia e privando queste ultime della loro consonante finale.
Tiebair=novecentodieci; miefaic=cinquecentoventi; sietaiz=ottocentonovanta;
fiekaid=duecentotrenta; piebair=seicentodieci.
6) I numeri formati da centinaia, decine e unit si ottengono, aggiungendo le unit alle decine e privando le decine e le centinaia della loro consonante finale.
Tiepailig=novecentosessantaquattro; liemaikid=quattrocentocinquantatre; piebaitiz=seicentodiciannove; miepailig=cinquecentosessantaquattrro; sietaibir=ottocentonovantuno; fiebaikid=duecontotredici; liefaific=quattrocentoventidue..
7) Dopo il 999, si ricorre al 1000 (vieb). Va fatto presente che negli ordini dal 1.000 in poi (come 10.000, 100.000, 1.000.000, ecc ), i quali sono tutti potenze del 10 e sono formati sempre da quattro lettere, la consonante finale indica una o pi terne di zeri da considerare nel numero, essendo esse consonanti numeriche, il cui valore ci ben noto. Inoltre, le consonanti c e z rappresentano rispettivamente uno zero e due zeri da aggiungersi al valore delle terne.
Se prendiamo vieb, ossia mille, la consonante numerica b (1) ci dice che gli zeri da aggiungere all unit sono tre (1x3). Non ci sono altri zeri da aggiungere, poich in esso mancano sia la consonante c (uno zero) sia la consonante z (due zeri). Infine i vari ordini vengono separati con un trattino. Ecco alcuni esempi:
Mille e due=vieb-fic; diecimila e quaranta=ciob-laig; centomila e trecento=ziub-kied; un milione=vief; un milione e trenta=vief-kaid; un milione e centomila=vief-ziub; un milione e centoquaranta=vief-bielaig; un milione e diecimilaquattro=vief-ciob-lig;
un miliardo e novanta=viek-taiz; dieci miliardi e un milionecinque=ciok-vief-mih; cento miliardi diecimilasettanta=ziuk-vief-raiv;
un bilione=viel; dieci bilioni e ottocentotre=ciol-siekid; centobilioni, diecimilioni e novecento=ziul-ciof-tiez;
un biliardo=viem; diecibiliardi=ciom; centobiliardi=zium; un biliardo, dieci miliardi e diecimila=viem-ciok-ciob;
un trilione=viep; dieci trilioni, cento biliardi e diecimila=ciop-zium-ciob; cento trilioni, dieci miliardi e centomilasettanta=ziup-ciok-ziub-raiv;
un triliardo=vier; cento triliardi, diecimilioni e centomila=ziur-ciof-ziub; un biliardo, dieci miliardi e centomila=viem-ciok-ziub;
un quadrilione=vies; dieci quadrilioni, cento bilioni, un milione e mille=cios-ziul-vief-vieb; cento quadrilioni, cento triliardi, diecibilioni e dieci milioni=zius-ziur-ciol-ciof;
un quadriliardo=viet; dieci quadriliardi, dieci trilioni e un miliardo=ciot-ciop-viek.
8) Gli ordini, dalle migliaia in poi, a volte sono preceduti dai numeri 2-999, che ne indicano la quantit . In quel caso tali numeri prendono il suffisso, che viene dato dalle ultime due cifre della potenza del 10 a cui si riferisce. L unione, comunque, avviene tramite la vocale i. Adesso vedremo come avviene con vari esempi.
Tremila=kidieb (dove kid 3 e eb la parte terminale di vieb (mille);
quarantotto milioni=laisixief (dove laisix=48, mentre ef la parte terminale di vief=un milione);
cinquantasei miliardi=maipiniok (dove maipin=56, mentre ek la parte terminale di viek=miliardo);
ottocentodieci bilioni=siebairiel (dove siebair=810, mentre el la parte terminale di iel=bilione);
duemilaquattrocento triliardi=ficieb-liegier (dove ficieb=2000, mentre eb la parte terminale di vieb=mille e er la parte terminale di
vier=triliardo)
9) Nella Raubser, i numeri hanno anche una forma letterale, che pu sostituire quella delle cifre. Le lettere, che vanno scritte in stampatello
maiuscolo, rappresentano le consonanti iniziali delle dieci cifre da 0 a 9. Essa riesce molto abbreviata, come possiamo renderci conto dai
seguenti esempi:
TFM=novecentoventicinque; BL=quattordici; SVR=ottocentosette; KP=trentasei; PKT=seicentotrentanove; FVS=duecentootto; FBV=duecentodieci;
TTT=novecentonovantanove; LBM=quattrocentoquindici.
Dal mille in poi, ogni ordine, dal pi grande al pi piccolo, viene indicato dalle due ultime lettere del suo nome (una vocale pi una
consonante). Inoltre, gli ordini vengono separati l uno dall altro con un trattino (-).
MEf=cinquemilioni; MOF=cinquantamilioni; MuF=cinquecentomilioni; KLREB-MFV=trecentoquarantasettemilacinquecentoventi;
KPEK-FVEF=trentaseimiliardi e ventimilioni; MFEK-SKEF-PEB=cinquantaduemiliardi, ottantatremilioni, seimilamila; REL-FEB-KLV=settebilioni,
duemila, trecentoquaranta; ecc
18) Numeri oltre i Miliardi
I Numeri oltre i Miliardi, che si possono esprimere con un nome, raggiungono grandezze superastronomiche. Basti pensare che il pi grande di essi, bitutit, rappresenta 104999, cio 1 seguito da 4999 zeri. Al riguardo, bisogna sapere che la formazione di tali numeri e l in terpretazione del loro valore si presen tano l una semplice e l altra agevole, per il fatto che essi sono stati ottenuti seguendo un criterio aritmetico basato sulla pura logica matematica. Perci cerchiamo di approfondire bene tale criterio. Ma, prima di continuare il discorso su tale argomento, ci conviene rivedere quanto gi appreso in precedenza. Ebbene, nei numeri potenze del 10 oltre i Miliardi, con esponente fino a 99, il bi iniziale indica la base 10; la sillaba che segue, la quale pu essere vi, bi, fi, ki, li mi, pi, ri, si, ti, indica le centinaia (il suo valore dato dalla consonante numerica); il numero formato dalle due consonanti numeriche finali, aggiunto alle centinaia, ci d l'esponente della base 10. In tali numeri e negli altri che seguiranno, l'accento cade sulla terzultima vocale. Vediamo alcuni esempi:
b vivif=102; b vibis=1018; b vifil=1024; b vikiv=1030; b vikip=1036; b vilif=1042; b vilis=1048; b vimil=1054; b vitit=1099.
B bivik=10103; b bifir=10127; b bilim=10145; b bimit=10159; b biriv=10170; b bikil=10134; b bibip=10116; b bipis=10168; b biviv=10100; b bisir=10187; b bitit=10199.
B fivis=10208; b fifip=10226; b filip=10246; b fipiv=10260; b firib=10271; b fikim=10235; b fibir=10217; b fipit=10269; b fiviv=10200; b fisis=10288; b fitit=10299.
B kivib=10301; b kifis=10328; b kilip=10346; b kipiv=10360; b kirib=10371; b kikim=10335; b kibir=10317; b kipit=10369; b kitif=10392; b kitit=10399.
B livil=10404; b lifis=10428; b lilip=10446; b lipiv=10460; b lirib=10471; b likim=10435; b libir= 10417; b lipip=10466; b litif=10492; b litit=10499.
b mivif=10502; b mibis=10518; b mifil=10524; b mikiv=10530; b mikip=10536; b milif=10542; b milis=10548; b mimil=10554; b mitit=10599.
B pivik=10603; b pifir=10627; b pilim=10645; b pimit=10659; b piriv=10670; b pikil=10634; b pibip=10616; b pipis=10668; b piviv=10600; b pisir=10687; b pitit=10699.
B rivis=10708; b rifip=10726; b rilip=10746; b ripiv=10760; b ririb=10771; b ri kim=10735; b ribir=10717; b ripit=10769; b riviv=10700; b risis=10788; b ritit=10799.
B sivib=10801; b sifis=10828; b silip=10846; b sipiv=10860; b sirib=10871; b sikim=10835; b sibir=10817; b sipit=10869; b sitif=10892; b sitit=10899.
B tivil=10904; b tifis=10928; b tilip=10946; b tipiv=10960; b tirib=10971; b tikim=10935; b tibir=10917; b tipip=10966; b titif=10992; b titit=10999.
In tali numeri vi, bi, fi, ki, li, mi, pi, ri, si e ti indicano le centinaia, poich corrispondono rispettivamente a 0, 100, 200, 300, 400, 500, 600, 700, 800 e 900. Ma, se alla i sostituiamo la a, facendoli diventare va, ba, fa, ka, la, ma, pa, ra, sa e ta, il loro valore aumenta di un migliaio, per cui essi diventano rispettivamente 1000, 1100, 1200, 1300, 1400, 1500, 1600, 1700, 1800 e 1900. Vediamo alcuni esempi:
b vabis=101018; b bafir=101127; b fasis=101288; b kalip=101346; b larib=101471; b mamil= 101554; b parib=101671; b rarib=101771; b sakim=101835; b tatit= 101999.
Se invece alla i sostituiamo la e e li facciamo diventare ve, be, fe, ke, le, me, pe, re, se e te, il loro valore aumenta di due migliaia, per cui essi diventano rispettivamente 2000, 2100, 2200, 2300, 2400, 2500, 2600, 2700, 2800 e 2900. Vediamo alcuni esempi:
b vebis=102018; b befir=102127; b fesis=102288; b kelip=102346; b lerib=102471; b memil=102554; b perib=102671; b rerib=102771; b sekim=102835; b tetit=102999.
Se invece alla i sostituiamo la o e li facciamo diventare vo, bo, fo, ko, lo, mo, po, ro, so e to, il loro valore aumenta di tre migliaia, per cui essi diventano rispettivamente 3000, 3100, 3200, 3300, 3400, 3500, 3600, 3700, 3800 e 3900. Vediamo alcuni esempi:
b vobis=103018; b bofir=103127; b fosis=103288; b kolip=103346; b lorib=103471; b momil=103554; b oerib=1023671; b rorib=103771; b sokim=103835; b totit=103999.
Se invece alla i sostituiamo la u e li facciamo diventare vu, bu, fu, ku, lu, mu, pu, ru, su e tu, il loro valore aumenta di quattro migliaia, per cui essi diventano rispettivamente 4000, 4100, 4200, 4300, 4400, 4500, 4600, 4700, 4800 e 4900. Vediamo alcuni esempi:
b vubis=104018; b bufir=104127; b fusis=104288; b kulip=104346; b lurib=104471; b mumil=104554; b purib=104671; b rurib=104771; b sukim=104835; b tutit=104999.
Se al posto di 1 c' un numero diverso, abbiamo:
Kid tao bivibik=3x1013 o 3 seguito da 13 zeri; riv tao bivibif=7x1012 o 7 seguito da 12 zeri; baif c tao bivibim=12x1015 o 12 seguito da 15 zeri; pin tao bivibis=6x1018 o 6 seguito da 18 zeri; ecc
Nelle potenze con base diversa da 10, abbiamo:
kid-xeibik=313; mih-xeivik=53; riv-xeibiv=710; baisix-xeivit=189.
(Come si vedr in seguito, il prefisso xei deriva da xeuz=potenza)
Oltre al nome, le potenze del 10 o di altri numeri, possono avere una forma letterale, che si ottiene nel modo seguente:
104=BVl; 93=Tk; 28=Fs; 10325=BVkfm; 10-25=BV-fm; 37x1032=KRxBVkf.
|
Nome |
Valore |
Suffisso |
Simbolo |
|
viev=unità |
100 |
v |
|
|
ciov=decina (deca) |
101 |
iov |
ov |
|
ziuv=centinaio (hecto) |
102 |
iuv |
uv |
|
vieb=migliaio |
103 |
ieb |
eb |
|
ciob=decamigliaio |
104 |
iob |
ob |
|
ziub=hectomigliaio |
105 |
iub |
ub |
|
vief=milione |
106 |
ief |
ef |
|
ciof=decamilione |
107 |
iof |
of |
|
ziuf=hectomilione |
108 |
iuf |
uf |
|
viek=miliardo |
109 |
iek |
ek |
|
ciok=decamiliardo |
1010 |
iok |
ok |
|
ziuk=hectomiliardo |
1011 |
iuk |
uk |
|
viel=bilione |
1012 |
iel |
el |
|
ciol=decabilione |
1013 |
iol |
ol |
|
ziul=hectobilione |
1014 |
iul |
ul |
|
viem=biliardo |
1015 |
iem |
em |
|
ciom=decabiliardo |
1016 |
iom |
om |
|
zium=hectobiliardo |
1017 |
ium |
um |
|
viep=trilione |
1018 |
iep |
ep |
|
ciop=decatrilione |
1019 |
iop |
op |
|
ziup=hectotrilione |
1020 |
iup |
up |
|
vier=triliardo |
1021 |
ier |
er |
|
cior=decatriliardo |
1022 |
ior |
or |
|
ziur=hectotriliardo |
1023 |
iur |
ur |
|
vies=quadrilione |
1024 |
ies |
es |
|
cios=decaquadrilione |
1025 |
ios |
os |
|
zius=hectoquadrilione |
1026 |
ius |
us |
|
viet=quadriliardo |
1027 |
iet |
et |
|
ciot=decaquadriliardo |
1028 |
iot |
ot |
|
ziut=hectoquadriliardo |
1029 |
iut |
ut |
|
Misura |
Valore |
Prefisso |
Simbolo |
|
voic=decimo |
10-1 |
voi |
vo |
|
vuiz=centesimo |
10-2 |
vui |
vu |
|
beiv=millesimo |
10-3 |
bei |
be |
|
boic=decimillesimo |
10-4 |
boi |
bo |
|
buiz=centimillesimo |
10-5 |
bui |
bu |
|
feiv=milionesimo |
10-6 |
fei |
fe |
|
foic=decimilionesimo |
10-7 |
foi |
fo |
|
fuiz=centimilionesimo |
10-8 |
fui |
fu |
|
keiv=miliardesimo |
10-9 |
kei |
ke |
|
koic=decimiliardesimo |
10-10 |
koi |
ko |
|
kuiz=centimiliardesimo |
10-11 |
kui |
ku |
|
leiv=bilionesimo |
10-12 |
lei |
le |
|
loic=decibilionesimo |
10-13 |
loi |
lo |
|
luiz=centibilionesimo |
10-14 |
lui |
lu |
|
meiv=biliardesimo |
10-15 |
mei |
me |
|
moic=decibiliardesimo |
10-16 |
moi |
mo |
|
muiz=centibiliardesimo |
10-17 |
mui |
mu |
|
peiv=trilionesimo |
10-18 |
pei |
pe |
|
poic=decitrilionesimo |
10-19 |
poi |
po |
|
puiz=centitrilionesimo |
10-20 |
pui |
pu |
|
reiv=triliardesimo |
10-21 |
rei |
re |
|
roic=decitriliardesimo |
10-22 |
roi |
ro |
|
ruiz=centitriliardesimo |
10-23 |
rui |
ru |
|
seiv=quadrilionesimo |
10-24 |
sei |
se |
|
soic=deciquadrilionesimo |
10-25 |
soi |
so |
|
suiz=centiquadrilionesimo |
10-26 |
sui |
su |
|
teiv=quadriliardesimo |
10-24 |
tei |
te |
|
toic=deciquadriliardesimo |
10-25 |
toi |
to |
|
tuiz=centiquadriliardesimo |
10-26 |
tui |
tu |
20) SISTEMA METRICO DECIMALE 1) Misure di Lunghezza I Multipli ed i Sottomultipli di neov (metro) si ottengono mediante i suffissi e i prefissi ottenuti con i nomi delle Potenze del 10 sia positive che negative.
Nel sistema metrico decimale, i multipli e i sottomultipli del metro (neov) e del grammo
(xod) si ottengono, prefissando i loro simboli (per ottenere i multipli) e suffissando i medesimi (per ottenere i sottomultipli) con i
prefissi e i suffissi riportati nelle due precedenti tabelle.
|
Nome |
Valore |
Abbreviazione |
Simbolo |
|
neov |
100 |
nev |
n |
|
neoviov=decametro |
101 |
niov |
nov |
|
neoviuv=hectometro |
102 |
niuv |
nuv |
|
neovieb=chilometro |
103 |
nieb |
neb |
|
neoviob=decachilometro |
104 |
niob |
nob |
|
neoviub=hectochilometro |
105 |
niub |
nub |
|
neovief=megametro |
106 |
nief |
nef |
|
neoviuf=decamegametro |
107 |
niof |
nof |
|
neoviuf=hectomegametro |
108 |
niuf |
nuf |
|
neoviek=gigametro |
109 |
niek |
nek |
|
neoviok=decagigametro |
10 |
niok |
nok |
|
neoviuk=hectogigametro |
1011 |
niuk |
nuk |
|
neoviel=terametro |
1012 |
niel |
nel |
|
neoviol=decaterametro |
1013 |
niol |
nol |
|
neoviul=hectoterametro |
1014 |
niul |
nul |
|
neoviem=petametro |
1015 |
niem |
nem |
|
neoviom=decapetametro |
1016 |
niom |
nom |
|
neovium=hectopetametro |
1017 |
nium |
num |
|
neoviep=exametro |
1018 |
niep |
nep |
|
neoviop=decaexametro |
1019 |
niop |
nop |
|
neoviup=hectoexametro |
1020 |
niup |
nup |
|
neovier=zettametro |
1021 |
nier |
ner |
|
neovior=decazettametro |
1022 |
nior |
nor |
|
neoviur=hectozettametro |
1023 |
niur |
nur |
|
neovies=yottametro |
1024 |
nies |
nes |
|
neovios=decayottametro |
1025 |
nios |
nos |
|
neovius=hectoyottametro |
1026 |
nius |
nus |
|
neoviet=yottametro |
1024 |
niet |
net |
|
neoviot=decayottametro |
1025 |
niot |
not |
|
neoviut=hectoyottametro |
1026 |
niut |
nut |
|
Nome |
Valore |
Abbreviazione |
Simbolo |
|
voineov=decimetro |
10-1 |
voin |
von |
|
vuineov=centimetro |
10-2 |
vuin |
vun |
|
beineov=millimetro |
10-3 |
bein |
ben |
|
boineov=decimillimetro |
10-4 |
boin |
bon |
|
buineov=centimillimetro |
10-5 |
buin |
bun |
|
feineov=micrometro |
10-6 |
fein |
fen |
|
foineov=decimicrometro |
10-7 |
foin |
fon |
|
fuineov=centimicrometro |
10-8 |
fuin |
fun |
|
keineov=nanometro |
10-9 |
kein |
ken |
|
koineov=decinanometro |
10-10 |
koink |
kon |
|
kuineov=centinanometro |
10-11 |
kuin |
kun |
|
leineov=picometro |
10-12 |
lein |
len |
|
loineovl=decipicometro |
10-13 |
loin |
lon |
|
luineov=centipicometro |
10-14 |
luin |
lun |
|
meineov=femtometro |
10-15 |
mein |
men |
|
moineov=decifemtometro |
10-16 |
moin |
mon |
|
muineov=centifemtometro |
10-17 |
muin |
mun |
|
peineov=attometro |
10-18 |
pein |
pen |
|
poineov=deciattometro |
10-19 |
poin |
pon |
|
puineov=centiattometro |
10-20 |
puin |
pun |
|
reineov=zeptometro |
10-21 |
rein |
ren |
|
roineov=decizeptometro |
10-22 |
roin |
ron |
|
ruineov=centizeptometro |
10-23 |
ruin |
run |
|
seineov=yoctometro |
10-24 |
sein |
sen |
|
soineov=deciyoctometro |
10-25 |
soin |
son |
|
teineov=centiyoctometro |
10-26 |
tein |
ten |
|
toineov=deciyoctometro |
10-25 |
toin |
ton |
|
tuineov=centiyoctometro |
10-26 |
tuin |
tun |
N.B. Aggiungendo alle Misure di Lunghezza la vocale o oppure la vocale u, si
ottengono le rispettive misure di superficie e di volume: 3) Misure di Massa
nev=metro / nevo=metro quadrato / nevu=metro cubo; voin=decametro / voino=decametro
quadrato / voinu=decametro cubo; niuv=centimetro / niuvo=centimetro quadrato / niuvu=centimetro
cubo.
2) Misure Agrarie di Superficie
Le Misure Agrarie di Superficie presentano un numero indicante i loro m2. Esse sono le seguenti:
Vavab=centiara; vavob=ara; vabuv=ettaro-a.
I Multipli e i Sottomultipli di xod (grammo) si ottengono mediante le consonanti numeriche, che vengono adoperate come potenze di 10 sia positive che negative.
|
Nome |
Valore |
Abbreviazione |
Simbolo |
|
xod |
100 |
x |
|
|
xodiov=decagrammo |
101 |
xiov |
xov |
|
xodiuv=hectogrammo |
102 |
xiuv |
xuv |
|
xodieb=chilogrammo |
103 |
xieb |
xeb |
|
xodiob=decachilogrammo |
104 |
xiob |
xob |
|
xodiub=hectochilogrammo |
105 |
xiub |
xub |
|
xodief=megagrammo |
106 |
xief |
xef |
|
xodiof=decamegagrammo |
107 |
xiof |
xof |
|
xodiuf=hectomegagrammo |
108 |
xiuf |
xuf |
|
xodiek=gigagrammo |
109 |
xiek |
xek |
|
xodiok=decagigagrammo |
1010 |
xiok |
xok |
|
xodiuk=hectogigagrammo |
1011 |
xiuk |
xuk |
|
xodiel=teragrammo |
1012 |
xiel |
xel |
|
xodiol=decateragrammo |
1013 |
xiol |
xol |
|
xodiul=hectoteragrammo |
1014 |
xuul |
xul |
|
xodiem=petagrammo |
1015 |
xiem |
xem |
|
xodiom=decapetagrammo |
1016 |
xiom |
xom |
|
xodium=hectopetagrammo |
1017 |
xium |
xum |
|
xodiep=exagrammo |
1018 |
xiep |
xep |
|
xodiop=decaexagrammo |
1019 |
xiop |
xop |
|
xodiup=hectoexagrammo |
1020 |
xiup |
xup |
|
xodier=zettagrammo |
1021 |
xier |
xer |
|
xodior=decazettagrammo |
1022 |
xior |
xor |
|
xodiur=hectozetagrammo |
1023 |
xiur |
xur |
|
xodies=yottagrammo |
1024 |
xies |
xes |
|
xodios=decayottagrammo |
1025 |
xios |
xos |
|
xodius=hectoyottagrammo |
1026 |
xius |
xus |
|
xodiet=yottagrammo |
1024 |
xiet |
xet |
|
xodiot=decayottagrammo |
1025 |
xiot |
xot |
|
xodiut=hectoyottagrammo |
1026 |
xiut |
xut |
|
Nome |
Valore |
Abbreviazione |
Simbolo |
|
voixod=decigrammo |
10-1 |
voix |
vox |
|
vuixod=centigrammo |
10-2 |
vuix |
vux |
|
beixod=milligrammo |
10-3 |
beix |
bex |
|
boixod=decimilligrammo |
10-4 |
boix |
box |
|
buixod=centimilligrammo |
10-5 |
buix |
bux |
|
feixod=microgrammo |
10-6 |
feix |
fex |
|
foixod=decimicrogrammo |
10-7 |
foix |
fox |
|
fuixod=centimicrogrammo |
10-8 |
fuix |
fux |
|
keixod=nanogrammo |
10-9 |
keix |
kex |
|
koixod=decinanogrammo |
10-10 |
koix |
kox |
|
kuixod=centinanogrammo |
10-11 |
kuix |
kux |
|
leixod=picogrammo |
10-12 |
leix |
lex |
|
loixod=decipicogrammo |
10-13 |
loix |
lox |
|
luixod=centipicogrammo |
10-14 |
luix |
lux |
|
meixod=femtogrammo |
10-15 |
meix |
mex |
|
moixod=decifemtogrammo |
10-16 |
moix |
mox |
|
muixod=centifemtogrammo |
10-17 |
muix |
mux |
|
peixod=attogrammo |
10-18 |
peix |
pex |
|
poixod=deciattogrammo |
10-19 |
poix |
pox |
|
puixod=centiattogrammo |
10-20 |
puix |
pux |
|
reixod=zeptogrammo |
10-21 |
reix |
rex |
|
roixod=decizeptogrammo |
10-22 |
roix |
rox |
|
ruixod=centizeptogrammo |
10-23 |
ruix |
rux |
|
seixod=yoctogrammo |
10-24 |
seix |
sex |
|
soixod=deciyoctogrammo |
10-25 |
soix |
sox |
|
suixod=centiyoctogrammo |
10-26 |
suix |
sux |
|
teixod=yoctogrammo |
10-24 |
teix |
tex |
|
toixod=deciyoctogrammo |
10-25 |
toix |
tox |
|
tuixod=centiyoctogrammo |
10-26 |
tuix |
tux |
4) Misure di Capacità MULTIPLI Nome Valore Abbreviazione
Simbolo guh=litro 100 g guhiov=decalitro 101 giov gov guhiuv=ettolitro 102 giuv guv guhieb=kilolitro 103 gieb geb SOTTOMULTIPLI Nome Valore Abbreviazione Simbolo voiguh=decilitro 10-1 voig vog vuiguh=centilitro 10-2 vuig vug beiguh=millilitro 10-3 beig beg 5) Ordini di grandezza del Tempo I multipli e i sottomultipli del
secondo (hag) sono riportati nella sottostante
tabella: MULTIPLI Nome Valore Simbolo hag=secondo 100 h hagiov=decasecondo 101 hov hagiuv=ettosecondo 102 huv hagieb=chilosecondo 103 heb hagief=megasecondo 106 hef hagiek=gigasecondo 109 hek hagiel=terasecondo 1012 hel hagiem=petasecondo 1015 hem hagiep=exsasecondo 1018 hep hagier=zettasecondo 1021 her hagies=yottasecondo 1024 hes hagiet=ennasecondo 1027 het SOTTOMULTIPLI Nome Valore Simbolo voihag=decisecondo 10-1 voh vuihag=centisecondo 10-2 vuh beihag=millisecondo 10-3 beh feihag=microsecondo 10-6 feh keihag=nanosecondo 10-9 keh leihag=picosecondo 10-12 leh meihag=femtosecondo 10-15 meh peihag=attosecondo 10-18 peh reihag=zeptosecondo 10-21 reh seihag=yoktosecondo 10-24 seh teihag=ennosecondo 10-27 teh
22) TABELLA DELLE POTENZE DEL 10 FINO ALL'ESPONENTE 1000
22) TABELLA DELLE POTENZE DEL 10 FINO ALL'ESPONENTE 1000
Biviviv=100 /
bivivib=101 /
bivivif=102 /
bivivik=103 /
bivivil=104 /
bivivim=105 /
bivivip=106 /
bivivir=107 /
bivivis=108 /
bivivit=109 /
bivibiv=1010
bivibib=1011 /
bivibif=1012 /
bivibik=1013 /
bivibil=1014 /
bivibim=1015 /
bivibip=1016 /
bivibir=1017 /
bivibis=1018 /
bivibit=1019 /
bivifiv=1020
bivifib=1021 /
bivifif=1022 /
bivifik=1023 /
bivifil=1024 /
bivifim=1025 /
bivifip=1026 /
bivifir=1027 /
bivifis=1028 /
bivifit=1028 /
bivikiv=1030
bivikib=1031 /
bivikif=1032 /
bivikik=1033 /
bivikil=1034 /
bivikim=1035 /
bivikip=1036 /
bivikir=1037 /
bivikis=1038 /
bivikit=1039 /
biviliv=1040
bivilib=1041 /
bivilif=1042 /
bivilik=1043 /
bivilil=1044 /
bivilim=1045 /
bivilip=1046 /
bivilir=1047 /
bivilis=1048 /
bivilit=1049 /
bivimiv=1050
bivimib=1051 /
bivimif=1052 /
bivimik=1053 /
bivimil=1054 /
bivimim=1055 /
bivimip=1056 /
bivimir=1057 /
bivimis=1058 /
bivimit=1059 /
bivipiv=1060
bivipib=1061 /
bivipif=1062 /
bivipik=1063 /
bivipil=1064 /
bivipim=1065 /
bivipip=1066 /
bivipir=1067 /
bivipis=1068 /
bivipit=1069 /
biviriv=1070
bivirib=1071 /
bivirif=1072 /
bivirik=1073 /
biviril=1074 /
bivirim=1075 /
bivirip=1076 /
bivirir=1077 /
biviris=1078 /
bivirit=1079 /
bivisiv=1080
bivisib=1081 /
bivisif=1082 /
bivisik=1083 /
bivisil=1084 /
bivisim=1085 /
bivisip=1086 /
bivisir=1087 /
bivisis=1088 /
bivisit=1089 /
bivitiv=1090
bivitib=1091 /
bivitif=1092 /
bivitik=1093 /
bivitil=1094 /
bivitim=1095 /
bivitip=1096 /
bivitir=1097 /
bivitis=1098 /
bivitit=1099 /
bibiviv=10100
bibivib=10101 /
bibivif=10102 /
bibivik=10103 /
bibivil=10104 /
bibivim=10105 /
bibivip=10106 /
bibivir=10107 /
bibivis=10108 /
bibivit=10109 /
bibibiv=10110
bibibib=10111 /
bibibif=10112 /
bibibik=10113 /
bibibil=10114 /
bibibim=10115 /
bibibip=10116 /
bibibir=10117 /
bibibis=10118 /
bibibit=10119 /
bibifiv=10120
bibifib=10121 /
bibifif=10122 /
bibifik=10123 /
bibifil=10124 /
bibifim=10125 /
bibifip=10126 /
bibifir=10127 /
bibifis=10128 /
bibifit=10128 /
bibikiv=10130
bibikib=10131 /
bibikif=10132 /
bibikik=10133 /
bibikil=10134 /
bibikim=10135 /
bibikip=10136 /
bibikir=10137 /
bibikis=10138 /
bibikit=10139 /
bibiliv=10140
bibilib=10141 /
bibilif=10142 /
bibilik=10143 /
bibilil=10144 /
bibilim=10145 /
bibilip=10146 /
bibilir=10147 /
bibilis=10148 /
bibilit=10149 /
bibimiv=10150
bibimib=10151 /
bibimif=10152 /
bibimik=10153 /
bibimil=10154 /
bibimim=10155 /
bibimip=10156 /
bibimir=10157 /
bibimis=10158 /
bibimit=10159 /
bibipiv=10160
bibipib=10161 /
bibipif=10162 /
bibipik=10163 /
bibipil=10164 /
bibipim=10165 /
bibipip=10166 /
bibipir=10167 /
bibipis=10168 /
bibipit=10169 /
bibiriv=10170
bibirib=10171 /
bibirif=10172 /
bibirik=10173 /
bibiril=10174 /
bibirim=10175 /
bibirip=10176 /
bibirir=10177 /
bibiris=10178 /
bibirit=10179 /
bibisiv=10180
bibisib=10181 /
bibisif=10182 /
bibisik=10183 /
bibisil=10184 /
bibisim=10185 /
bibisip=10186 /
bibisir=10187 /
bibasis=10188 /
bibasit=10189 /
bibativ=10190
bibatib=10191 /
bibatif=10192 /
bibatik=10193 /
bibatil=10194 /
bibatim=10195 /
bibatip=10196 /
bibatir=10197 /
bibatis=10198 /
bibitit=10199 /
bifiviv=10200
bifivib=10201 /
bifivif=10202 /
bifivik=10203 /
bifivil=10204 /
bifivim=10205 /
bifivip=10206 /
bifivir=10207 /
bifivis=10208 /
bifivit=10209 /
bifiviv=10210
bifibib=10211 /
bifibif=10212 /
bifibik=10213 /
bifibil=10214 /
bifibim=10215 /
bifibip=10216 /
bifibir=10217 /
bifibis=10218 /
bifibit=10219 /
bififiv=10220
bififib=10221 /
bififif=10222 /
bififik=10223 /
bififil=10224 /
bififim=10225 /
bififip=10226 /
bififir=10227 /
bififis=10228 /
bififit=10228 /
bifikiv=10230
bifikib=10231 /
bifikif=10232 /
bifikik=10233 /
bifikil=10234 /
bifikim=10235 /
bifikip=10236 /
bifikir=10237 /
bifikis=10238 /
bifikit=10239 /
bifiliv=10240
bifilib=10241 /
bifilif=10242 /
bifilik=10243 /
bifilil=10244 /
bifilim=10245 /
bifilip=10246 /
bifilir=10247 /
bifilis=10248 /
bifilit=10249 /
bifimiv=10250
bifimib=10251 /
bifimif=10252 /
bifimik=10253 /
bifimil=10254 /
bifimim=10255 /
bifimip=10256 /
bifimir=10257 /
bifimis=10258 /
bifimit=10259 /
bifipiv=10260
bifipib=10261 /
bifipif=10262 /
bifipik=10263 /
bifipil=10264 /
bifipim=10265 /
bifipip=10266 /
bifipir=10267 /
bifipis=10268 /
bifipit=10269 /
bifiriv=10270
bifirib=10271 /
bifirif=10272 /
bifirik=10273 /
bifiril=10274 /
bifirim=10275 /
bifirip=10276 /
bifirir=10277 /
bifiris=10278 /
bifirit=10279 /
bifisiv=10280
bifisib=10281 /
bifisif=10282 /
bifisik=10283 /
bifisil=10284 /
bifisim=10285 /
bifisip=10286 /
bifisir=10287 /
bifisis=10288 /
bifisit=10289 /
bifitiv=10280
bifitib=10281 /
bifitif=10282 /
bifitik=10283 /
bifitil=10284 /
bifitim=10285 /
bifitip=10286 /
bifitir=10287 /
bifitis=10288 /
bifitit=10289 /
bikiviv=10300
bikivib=10301 /
bikivif=10302 /
bikivik=10303 /
bikivil=10304 /
bikivim=10305 /
bikivip=10306 /
bikivir=10307 /
bikivis=10308 /
bikivit=10309 /
bikiviv=10310
bikibib=10311 /
bikibif=10312 /
bikibik=10313 /
bikibil=10314 /
bikibim=10315 /
bikibip=10316 /
bikibir=10317 /
bikibis=10318 /
bikibit=10319 /
bikifiv=10320
bikifib=10321 /
bikifif=10322 /
bikifik=10323 /
bikifil=10324 /
bikifim=10325 /
bikifip=10326 /
bikifir=10327 /
bikifis=10328 /
bikifit=10328 /
bikikiv=10330
bikikib=10331 /
bikikif=10332 /
bikikik=10 /
bikikil=10334 /
bikikim=10335 /
bikikip=10336 /
bikikir=10337 /
bikikis=10338 /
bikikit=10339 /
bikiliv=10340
bikilib=10341 /
bikilif=10342 /
bikilik=10343 /
bikilil=10344 /
bikilim=10345 /
bikilip=10346 /
bikilir=10347 /
bikilis=10348 /
bikilit=10349 /
bikimiv=10350
bikimib=10351 /
bikimif=10352 /
bikimik=10353 /
bikimil=10354 /
bikimim=10355 /
bikimip=10356 /
bikimir=10357 /
bikimis=10358 /
bikimit=10359 /
bikipiv=10360
bikipib=10361 /
bikipif=10362 /
bikipik=10363 /
bikipil=10364 /
bikipim=10365 /
bikipip=10366 /
bikipir=10367 /
bikipis=10368 /
bikipit=10369 /
bikiriv=10370
bikirib=10371 /
bikirif=10372 /
bikirik=10373 /
bikiril=10374 /
bikirim=10375 /
bikirip=10376 /
bikirir=10377 /
bikiris=10378 /
bikirit=10379 /
bikisiv=10380
bikisib=10381 /
bikisif=10382 /
bikisik=10383 /
bikisil=10384 /
bikisim=10385 /
bikisip=10386 /
bikisir=10387 /
bikisis=10388 /
bikisit=10389 /
bikitiv=10390
bikitib=10391 /
bikitif=10392 /
bikitik=10393 /
bikitil=10394 /
bikitim=10395 /
bikitip=10396 /
bikitir=10397 /
bikitis=10398 /
bikitit=10399 /
biliviv=10400
bilivib=10401 /
bilivif=10402 /
bilivik=10403 /
bilivil=10404 /
bilivim=10405 /
bilivip=10406 /
bilivir=10407 /
bilivis=10408 /
bilivit=10409 /
bilibiv=10410
bilibib=10411 /
bilibif=10412 /
bilibik=10413 /
bilibil=10414 /
bilibim=10415 /
bilibip=10416 /
bilibir=10417 /
bilibis=10418 /
bilibit=10419 /
bilifiv=10420
bilifib=10421 /
bilifif=10422 /
bilifik=10423 /
bilifil=10424 /
bilifim=10425 /
bilifip=10426 /
bilifir=10427 /
bilifis=10428 /
bilifit=10428 /
bilikiv=10430
bilikib=10431 /
bilikif=10432 /
bilikik=10433 /
bilikil=10434 /
bilikim=10435 /
bilikip=10436 /
bilikir=10437 /
bilikis=10438 /
bilikit=10439 /
bililiv=10440
bililib=10441 /
bililif=10442 /
bililik=10443 /
bililil=10444 /
bililim=10445 /
bililip=10446 /
bililir=10447 /
bililis=10448 /
bililit=10449 /
bilimiv=10450
bilimib=10451 /
bilimif=10452 /
bilimik=10453 /
bilimil=10454 /
bilimim=10455 /
bilimip=10456 /
bilimir=10457 /
bilimis=10458 /
bilimit=10459 /
bilipiv=10460
bilipib=10461 /
bilipif=10462 /
bilipik=10463 /
bilipil=10464 /
bilipim=10465 /
bilipip=10466 /
bilipir=10467 /
bilipis=10468 /
bilipit=10469 /
biliriv=10470
bilirib=10471 /
bilirif=10472 /
bilirik=10473 /
biliril=10474 /
bilirim=10475 /
bilirip=10476 /
bilirir=10477 /
biliris=10478 /
bilirit=10479 /
bilisiv=10480
bilisib=10481 /
bilisif=10482 /
bilisik=10483 /
bilisil=10484 /
bilisim=10485 /
bilisip=10486 /
bilisir=10487 /
bilisis=10488 /
bilisit=10489 /
bilitiv=10490
bilitib=10491 /
bilitif=10492 /
bilitik=10493 /
bilitil=10494 /
bilitim=10495 /
bilitip=10496 /
bilitir=10497 /
bilitis=10498 /
bilitit=10499 /
Bimiviv=10500
Bimivib=10501 /
Bimivif=10502 /
Bimivik=10503 /
Bimivil=10504 /
Bimivim=10505 /
Bimivip=10506 /
Bimivir=10507 /
Bimivis=10508 /
Bimivit=10509 /
Bimibiv=10510
bimibib=10511 /
bimibif=10512 /
bimibik=10513 /
bimibil=10514 /
bimibim=10515 /
bimibip=10516 /
bimibir=10517 /
bimibis=10518 /
bimibit=10519 /
bimifiv=10520
bimifib=10521 /
bimifif=10522 /
bimifik=10523 /
bimifil=10524 /
bimifim=10525 /
bimifip=10526 /
bimifir=10527 /
bimifis=10528 /
bimifit=10528 /
bimikiv=10530
bimikib=10531 /
bimikif=10532 /
bimikik=10533 /
bimikil=10534 /
bimikim=10535 /
bimikip=10536 /
bimikir=10537 /
bimikis=10538 /
bimikit=10539 /
bimiliv=10540
bimilib=10541 /
bimilif=10542 /
bimilik=10543 /
bimilil=10544 /
bimilim=10545 /
bimilip=10546 /
bimilir=10547 /
bimilis=10548 /
bimilit=10549 /
bimimiv=10550
bimimib=10551 /
bimimif=10552 /
bimimik=10553 /
bimimil=10554 /
bimimim=10555 /
bimimip=10556 /
bimimir=10557 /
bimimis=10558 /
bimimit=10559 /
bimipiv=10560
bimipib=10561 /
bimipif=10562 /
bimipik=10563 /
bimipil=10564 /
bimipim=10565 /
bimipip=10566 /
bimipir=10567 /
bimipis=10568 /
bimipit=10569 /
bimiriv=10570
bimirib=10571 /
bimirif=10572 /
bimirik=10573 /
bimiril=10574 /
bimirim=10575 /
bimirip=10576 /
bimirir=10577 /
bimiris=10578 /
bimirit=10579 /
bimisiv=10580
bimisib=10581 /
bimisif=10582 /
bimisik=10583 /
bimisil=10584 /
bimisim=10585 /
bimisip=10586 /
bimisir=10587 /
bimisis=10588 /
bimisit=10589 /
bimitiv=10590
bimitib=10591 /
bimitif=10592 /
bimitik=10593 /
bimitil=10594 /
bimitim=10595 /
bimitip=10596 /
bimitir=10597 /
bimitis=10598 /
bimitit=10599 /
bipiviv=10600
bipivib=10601 /
bipivif=10602 /
bipivik=10603 /
bipivil=10604 /
bipivim=10605 /
bipivip=10606 /
bipivir=10607 /
bipivis=10608 /
bipivit=10609 /
bipibiv=10610
bipibib=10611 /
bipibif=10612 /
bipibik=10613 /
bipibil=10614 /
bipibim=10615 /
bipibip=10616 /
bipibir=10617 /
bipibis=10618 /
bipibit=10619 /
bipifiv=10620
bipifib=10621 /
bipifif=10622 /
bipifik=10623 /
bipifil=10624 /
bipifim=10625 /
bipifip=10626 /
bipifir=10627 /
bipifis=10628 /
bipifit=10628 /
bipikiv=10630
bipikib=10631 /
bipikif=10632 /
bipikik=10633 /
bipikil=10634 /
bipikim=10635 /
bipikip=10636 /
bipikir=10637 /
bipikis=10638 /
bipikit=10639 /
bipiliv=10640
bipilib=10641 /
bipilif=10642 /
bipilik=10643 /
bipilil=10644 /
bipilim=10645 /
bipilip=10646 /
bipilir=10647 /
bipilis=10648 /
bipilit=10649 /
bipimiv=10650
bipimib=10651 /
bipimif=10652 /
bipimik=10653 /
bipimil=10654 /
bipimim=10655 /
bipimip=10656 /
bipimir=10657 /
bipimis=10658 /
bipimit=10659 /
bipipiv=10660
bipipib=10661 /
bipipif=10662 /
bipipik=10663 /
bipipil=10664 /
bipipim=10665 /
bipipip=10666 /
bipipir=10667 /
bipipis=10668 /
bipipit=10669 /
bipiriv=10670
bipirib=10671 /
bipirif=10672 /
bipirik=10673 /
bipiril=10674 /
bipirim=10675 /
bipirip=10676 /
bipirir=10677 /
bipiris=10678 /
bipirit=10679 /
bipisiv=10680
bipisib=10681 /
bipisif=10682 /
bipisik=10683 /
bipisil=10684 /
bipisim=10685 /
bipisip=10686 /
bipisir=10687 /
bipisis=10688 /
bipisit=10689 /
bipitiv=10690
bipitib=10691 /
bipitif=10692 /
bipitik=10693 /
bipitil=10694 /
bipitim=10695 /
bipitip=10696 /
bipitir=10697 /
bipitis=10698 /
bipitit=10699 /
biriviv=10700
birivib=10701 /
birivif=10702 /
birivik=10703 /
birivil=10704 /
birivim=10705 /
birivip=10706 /
birivir=10707 /
birivis=10708 /
birivit=10709 /
biriviv=10710
biribib=10711 /
biribif=10712 /
biribik=10713 /
biribil=10714 /
biribim=10715 /
biribip=10716 /
biribir=10717 /
biribis=10718 /
biribit=10719 /
birifiv=10720
birifib=10721 /
birifif=10722 /
birifik=10723 /
birifil=10724 /
birifim=10725 /
birifip=10726 /
birifir=10727 /
birifis=10728 /
birifit=10728 /
birikiv=10730
birikib=10731 /
birikif=10732 /
birikik=10733 /
birikil=10734 /
birikim=10735 /
birikip=10736 /
birikir=10737 /
birikis=10738 /
birikit=10739 /
biriliv=10740
birilib=10741 /
birilif=10742 /
birilik=10743 /
birilil=10744 /
birilim=10745 /
birilip=10746 /
birilir=10747 /
birilis=10748 /
birilit=10749 /
birimiv=10750
birimib=10751 /
birimif=10752 /
birimik=10753 /
birimil=10754 /
birimim=10755 /
birimip=10756 /
birimir=10757 /
birimis=10758 /
birimit=10759 /
biripiv=10760
biripib=10761 /
biripif=10762 /
biripik=10763 /
biripil=10764 /
biripim=10765 /
biripip=10766 /
biripir=10767 /
biripis=10768 /
biripit=10769 /
biririv=10770
biririb=10771 /
biririf=10772 /
biririk=10773 /
biriril=10774 /
biririm=10775 /
biririp=10776 /
biririr=10777 /
biriris=10778 /
biririt=10779 /
birisiv=10780
birisib=10781 /
birisif=10782 /
birisik=10783 /
birisil=10784 /
birisim=10785 /
birisip=10786 /
birisir=10787 /
birisis=10788 /
birisit=10789 /
biritiv=10790
biritib=10791 /
biritif=10792 /
biritik=10793 /
biritil=10794 /
biritim=10795 /
biritip=10796 /
biritir=10797 /
biritis=10798 /
biritit=10799 /
bisiviv=10800
bisivib=10801 /
bisivif=10802 /
bisivik=10803 /
bisivil=10804 /
bisivim=10805 /
bisivip=10806 /
bisivir=10807 /
bisivis=10808 /
bisivit=10809 /
bisiviv=10810
bisibib=10811 /
bisibif=10812 /
bisibik=10813 /
bisibil=10814 /
bisibim=10815 /
bisibip=10816 /
bisibir=10817 /
bisibis=10818 /
bisibit=10819 /
bisifiv=10820
bisifib=10821 /
bisifif=10822 /
bisifik=10823 /
bisifil=10824 /
bisifim=10825 /
bisifip=10826 /
bisifir=10827 /
bisifis=10828 /
bisifit=10828 /
bisikiv=10830
bisikib=10831 /
bisikif=10832 /
bisikik=10833 /
bisikil=10834 /
bisikim=10835 /
bisikip=10836 /
bisikir=10837 /
bisikis=10838 /
bisikit=10839 /
bisiliv=10840
bisilib=10841 /
bisilif=10842 /
bisilik=10843 /
bisilil=10844 /
bisilim=10845 /
bisilip=10846 /
bisilir=10847 /
bisilis=10848 /
bisilit=10849 /
bisimiv=10850
bisimib=10851 /
bisimif=10852 /
bisimik=10853 /
bisimil=10854 /
bisimim=10855 /
bisimip=10856 /
bisimir=10857 /
bisimis=10858 /
bisimit=10859 /
bisipiv=10860
bisipib=10861 /
bisipif=10862 /
bisipik=10863 /
bisipil=10864 /
bisipim=10865 /
bisipip=10866 /
bisipir=10867 /
bisipis=10868 /
bisipit=10869 /
bisiriv=10870
bisirib=10871 /
bisirif=10872 /
bisirik=10873 /
bisiril=10874 /
bisirim=10875 /
bisirip=10876 /
bisirir=10877 /
bisiris=10878 /
bisirit=10879 /
bisisiv=10880
bisisib=10881 /
bisisif=10882 /
bisisik=10883 /
bisisil=10884 /
bisisim=10885 /
bisisip=10886 /
bisisir=10887 /
bisisis=10888 /
bisisit=10889 /
bisitiv=10890
bisitib=10891 /
bisitif=10892 /
bisitik=10893 /
bisitil=10894 /
bisitim=10895 /
bisitip=10896 /
bisitir=10897 /
bisitis=10898 /
bisitit=10899 /
bitiviv=10900
bitivib=10901 /
bitivif=10902 /
bitivik=10903 /
bitivil=10904 /
bitivim=10905 /
bitivip=10906 /
bitivir=10907 /
bitivis=10908 /
bitivit=10909 /
bitibiv=10910
bitibib=10911 /
bitibif=10912 /
bitibik=10913 /
bitibil=10914 /
bitibim=10915 /
bitibip=10916 /
bitibir=10917 /
bitibis=10918 /
bitibit=10919 /
bitifiv=10920
bitifib=10921 /
bitifif=10922 /
bitifik=10923 /
bitifil=10924 /
bitifim=10925 /
bitifip=10926 /
bitifir=10927 /
bitifis=10928 /
bitifit=10928 /
bitikiv=10930
bitikib=10931 /
bitikif=10932 /
bitikik=10933 /
bitikil=10934 /
bitikim=10935 /
bitikip=10936 /
bitikir=10937 /
bitikis=10938 /
bitikit=10939 /
bitiliv=10940
bitilib=10941 /
bitilif=10942 /
bitilik=10943 /
bitilil=10944 /
bitilim=10945 /
bitilip=10946 /
bitilir=10947 /
bitilis=10948 /
bitilit=10949 /
bitimiv=10950
bitimib=10951 /
bitimif=10952 /
bitimik=10953 /
bitimil=10954 /
bitimim=10955 /
bitimip=10956 /
bitimir=10957 /
bitimis=10958 /
bitimit=10959 /
bitipiv=10960
bitipib=10961 /
bitipif=10962 /
bitipik=10963 /
bitipil=10964 /
bitipim=10965 /
bitipip=10966 /
bitipir=10967 /
bitipis=10968 /
bitipit=10969 /
bitiriv=10970
bitirib=10971 /
bitirif=10972 /
bitirik=10973 /
bitiril=10974 /
bitirim=10975 /
bitirip=10976 /
bitirir=10977 /
bitiris=10978 /
bitirit=10979 /
bitisiv=10980
bitisib=10981 /
bitisif=10982 /
bitisik=10983 /
bitisil=10984 /
bitisim=10985 /
bitisip=10986 /
bitisir=10987 /
bitisis=10988 /
bitisit=10989 /
bititiv=10990
bititib=10991 /
bititif=10992 /
bititik=10993 /
bititil=10994 /
bititim=10995 /
bititip=10996 /
bititir=10997 /
bititis=10998 /
bititit=10999 /
bivaviv=101000 /
Biviviv=100 /
bivivib=101 /
bivivif=102 /
bivivik=103 /
bivivil=104 /
bivivim=105 /
bivivip=106 /
bivivir=107 /
bivivis=108 /
bivivit=109 /
bivibiv=1010
bivibib=1011 /
bivibif=1012 /
bivibik=1013 /
bivibil=1014 /
bivibim=1015 /
bivibip=1016 /
bivibir=1017 /
bivibis=1018 /
bivibit=1019 /
bivifiv=1020
bivifib=1021 /
bivifif=1022 /
bivifik=1023 /
bivifil=1024 /
bivifim=1025 /
bivifip=1026 /
bivifir=1027 /
bivifis=1028 /
bivifit=1028 /
bivikiv=1030
bivikib=1031 /
bivikif=1032 /
bivikik=1033 /
bivikil=1034 /
bivikim=1035 /
bivikip=1036 /
bivikir=1037 /
bivikis=1038 /
bivikit=1039 /
biviliv=1040
bivilib=1041 /
bivilif=1042 /
bivilik=1043 /
bivilil=1044 /
bivilim=1045 /
bivilip=1046 /
bivilir=1047 /
bivilis=1048 /
bivilit=1049 /
bivimiv=1050
bivimib=1051 /
bivimif=1052 /
bivimik=1053 /
bivimil=1054 /
bivimim=1055 /
bivimip=1056 /
bivimir=1057 /
bivimis=1058 /
bivimit=1059 /
bivipiv=1060
bivipib=1061 /
bivipif=1062 /
bivipik=1063 /
bivipil=1064 /
bivipim=1065 /
bivipip=1066 /
bivipir=1067 /
bivipis=1068 /
bivipit=1069 /
biviriv=1070
bivirib=1071 /
bivirif=1072 /
bivirik=1073 /
biviril=1074 /
bivirim=1075 /
bivirip=1076 /
bivirir=1077 /
biviris=1078 /
bivirit=1079 /
bivisiv=1080
bivisib=1081 /
bivisif=1082 /
bivisik=1083 /
bivisil=1084 /
bivisim=1085 /
bivisip=1086 /
bivisir=1087 /
bivisis=1088 /
bivisit=1089 /
bivitiv=1090
bivitib=1091 /
bivitif=1092 /
bivitik=1093 /
bivitil=1094 /
bivitim=1095 /
bivitip=1096 /
bivitir=1097 /
bivitis=1098 /
bivitit=1099 /
bibiviv=10100
bibivib=10101 /
bibivif=10102 /
bibivik=10103 /
bibivil=10104 /
bibivim=10105 /
bibivip=10106 /
bibivir=10107 /
bibivis=10108 /
bibivit=10109 /
bibibiv=10110
bibibib=10111 /
bibibif=10112 /
bibibik=10113 /
bibibil=10114 /
bibibim=10115 /
bibibip=10116 /
bibibir=10117 /
bibibis=10118 /
bibibit=10119 /
bibifiv=10120
bibifib=10121 /
bibifif=10122 /
bibifik=10123 /
bibifil=10124 /
bibifim=10125 /
bibifip=10126 /
bibifir=10127 /
bibifis=10128 /
bibifit=10128 /
bibikiv=10130
bibikib=10131 /
bibikif=10132 /
bibikik=10133 /
bibikil=10134 /
bibikim=10135 /
bibikip=10136 /
bibikir=10137 /
bibikis=10138 /
bibikit=10139 /
bibiliv=10140
bibilib=10141 /
bibilif=10142 /
bibilik=10143 /
bibilil=10144 /
bibilim=10145 /
bibilip=10146 /
bibilir=10147 /
bibilis=10148 /
bibilit=10149 /
bibimiv=10150
bibimib=10151 /
bibimif=10152 /
bibimik=10153 /
bibimil=10154 /
bibimim=10155 /
bibimip=10156 /
bibimir=10157 /
bibimis=10158 /
bibimit=10159 /
bibipiv=10160
bibipib=10161 /
bibipif=10162 /
bibipik=10163 /
bibipil=10164 /
bibipim=10165 /
bibipip=10166 /
bibipir=10167 /
bibipis=10168 /
bibipit=10169 /
bibiriv=10170
bibirib=10171 /
bibirif=10172 /
bibirik=10173 /
bibiril=10174 /
bibirim=10175 /
bibirip=10176 /
bibirir=10177 /
bibiris=10178 /
bibirit=10179 /
bibisiv=10180
bibisib=10181 /
bibisif=10182 /
bibisik=10183 /
bibisil=10184 /
bibisim=10185 /
bibisip=10186 /
bibisir=10187 /
bibasis=10188 /
bibasit=10189 /
bibativ=10190
bibatib=10191 /
bibatif=10192 /
bibatik=10193 /
bibatil=10194 /
bibatim=10195 /
bibatip=10196 /
bibatir=10197 /
bibatis=10198 /
bibitit=10199 /
bifiviv=10200
bifivib=10201 /
bifivif=10202 /
bifivik=10203 /
bifivil=10204 /
bifivim=10205 /
bifivip=10206 /
bifivir=10207 /
bifivis=10208 /
bifivit=10209 /
bifiviv=10210
bifibib=10211 /
bifibif=10212 /
bifibik=10213 /
bifibil=10214 /
bifibim=10215 /
bifibip=10216 /
bifibir=10217 /
bifibis=10218 /
bifibit=10219 /
bififiv=10220
bififib=10221 /
bififif=10222 /
bififik=10223 /
bififil=10224 /
bififim=10225 /
bififip=10226 /
bififir=10227 /
bififis=10228 /
bififit=10228 /
bifikiv=10230
bifikib=10231 /
bifikif=10232 /
bifikik=10233 /
bifikil=10234 /
bifikim=10235 /
bifikip=10236 /
bifikir=10237 /
bifikis=10238 /
bifikit=10239 /
bifiliv=10240
bifilib=10241 /
bifilif=10242 /
bifilik=10243 /
bifilil=10244 /
bifilim=10245 /
bifilip=10246 /
bifilir=10247 /
bifilis=10248 /
bifilit=10249 /
bifimiv=10250
bifimib=10251 /
bifimif=10252 /
bifimik=10253 /
bifimil=10254 /
bifimim=10255 /
bifimip=10256 /
bifimir=10257 /
bifimis=10258 /
bifimit=10259 /
bifipiv=10260
bifipib=10261 /
bifipif=10262 /
bifipik=10263 /
bifipil=10264 /
bifipim=10265 /
bifipip=10266 /
bifipir=10267 /
bifipis=10268 /
bifipit=10269 /
bifiriv=10270
bifirib=10271 /
bifirif=10272 /
bifirik=10273 /
bifiril=10274 /
bifirim=10275 /
bifirip=10276 /
bifirir=10277 /
bifiris=10278 /
bifirit=10279 /
bifisiv=10280
bifisib=10281 /
bifisif=10282 /
bifisik=10283 /
bifisil=10284 /
bifisim=10285 /
bifisip=10286 /
bifisir=10287 /
bifisis=10288 /
bifisit=10289 /
bifitiv=10280
bifitib=10281 /
bifitif=10282 /
bifitik=10283 /
bifitil=10284 /
bifitim=10285 /
bifitip=10286 /
bifitir=10287 /
bifitis=10288 /
bifitit=10289 /
bikiviv=10300
bikivib=10301 /
bikivif=10302 /
bikivik=10303 /
bikivil=10304 /
bikivim=10305 /
bikivip=10306 /
bikivir=10307 /
bikivis=10308 /
bikivit=10309 /
bikiviv=10310
bikibib=10311 /
bikibif=10312 /
bikibik=10313 /
bikibil=10314 /
bikibim=10315 /
bikibip=10316 /
bikibir=10317 /
bikibis=10318 /
bikibit=10319 /
bikifiv=10320
bikifib=10321 /
bikifif=10322 /
bikifik=10323 /
bikifil=10324 /
bikifim=10325 /
bikifip=10326 /
bikifir=10327 /
bikifis=10328 /
bikifit=10328 /
bikikiv=10330
bikikib=10331 /
bikikif=10332 /
bikikik=10 /
bikikil=10334 /
bikikim=10335 /
bikikip=10336 /
bikikir=10337 /
bikikis=10338 /
bikikit=10339 /
bikiliv=10340
bikilib=10341 /
bikilif=10342 /
bikilik=10343 /
bikilil=10344 /
bikilim=10345 /
bikilip=10346 /
bikilir=10347 /
bikilis=10348 /
bikilit=10349 /
bikimiv=10350
bikimib=10351 /
bikimif=10352 /
bikimik=10353 /
bikimil=10354 /
bikimim=10355 /
bikimip=10356 /
bikimir=10357 /
bikimis=10358 /
bikimit=10359 /
bikipiv=10360
bikipib=10361 /
bikipif=10362 /
bikipik=10363 /
bikipil=10364 /
bikipim=10365 /
bikipip=10366 /
bikipir=10367 /
bikipis=10368 /
bikipit=10369 /
bikiriv=10370
bikirib=10371 /
bikirif=10372 /
bikirik=10373 /
bikiril=10374 /
bikirim=10375 /
bikirip=10376 /
bikirir=10377 /
bikiris=10378 /
bikirit=10379 /
bikisiv=10380
bikisib=10381 /
bikisif=10382 /
bikisik=10383 /
bikisil=10384 /
bikisim=10385 /
bikisip=10386 /
bikisir=10387 /
bikisis=10388 /
bikisit=10389 /
bikitiv=10390
bikitib=10391 /
bikitif=10392 /
bikitik=10393 /
bikitil=10394 /
bikitim=10395 /
bikitip=10396 /
bikitir=10397 /
bikitis=10398 /
bikitit=10399 /
biliviv=10400
bilivib=10401 /
bilivif=10402 /
bilivik=10403 /
bilivil=10404 /
bilivim=10405 /
bilivip=10406 /
bilivir=10407 /
bilivis=10408 /
bilivit=10409 /
bilibiv=10410
bilibib=10411 /
bilibif=10412 /
bilibik=10413 /
bilibil=10414 /
bilibim=10415 /
bilibip=10416 /
bilibir=10417 /
bilibis=10418 /
bilibit=10419 /
bilifiv=10420
bilifib=10421 /
bilifif=10422 /
bilifik=10423 /
bilifil=10424 /
bilifim=10425 /
bilifip=10426 /
bilifir=10427 /
bilifis=10428 /
bilifit=10428 /
bilikiv=10430
bilikib=10431 /
bilikif=10432 /
bilikik=10433 /
bilikil=10434 /
bilikim=10435 /
bilikip=10436 /
bilikir=10437 /
bilikis=10438 /
bilikit=10439 /
bililiv=10440
bililib=10441 /
bililif=10442 /
bililik=10443 /
bililil=10444 /
bililim=10445 /
bililip=10446 /
bililir=10447 /
bililis=10448 /
bililit=10449 /
bilimiv=10450
bilimib=10451 /
bilimif=10452 /
bilimik=10453 /
bilimil=10454 /
bilimim=10455 /
bilimip=10456 /
bilimir=10457 /
bilimis=10458 /
bilimit=10459 /
bilipiv=10460
bilipib=10461 /
bilipif=10462 /
bilipik=10463 /
bilipil=10464 /
bilipim=10465 /
bilipip=10466 /
bilipir=10467 /
bilipis=10468 /
bilipit=10469 /
biliriv=10470
bilirib=10471 /
bilirif=10472 /
bilirik=10473 /
biliril=10474 /
bilirim=10475 /
bilirip=10476 /
bilirir=10477 /
biliris=10478 /
bilirit=10479 /
bilisiv=10480
bilisib=10481 /
bilisif=10482 /
bilisik=10483 /
bilisil=10484 /
bilisim=10485 /
bilisip=10486 /
bilisir=10487 /
bilisis=10488 /
bilisit=10489 /
bilitiv=10490
bilitib=10491 /
bilitif=10492 /
bilitik=10493 /
bilitil=10494 /
bilitim=10495 /
bilitip=10496 /
bilitir=10497 /
bilitis=10498 /
bilitit=10499 /
Bimiviv=10500
Bimivib=10501 /
Bimivif=10502 /
Bimivik=10503 /
Bimivil=10504 /
Bimivim=10505 /
Bimivip=10506 /
Bimivir=10507 /
Bimivis=10508 /
Bimivit=10509 /
Bimibiv=10510
bimibib=10511 /
bimibif=10512 /
bimibik=10513 /
bimibil=10514 /
bimibim=10515 /
bimibip=10516 /
bimibir=10517 /
bimibis=10518 /
bimibit=10519 /
bimifiv=10520
bimifib=10521 /
bimifif=10522 /
bimifik=10523 /
bimifil=10524 /
bimifim=10525 /
bimifip=10526 /
bimifir=10527 /
bimifis=10528 /
bimifit=10528 /
bimikiv=10530
bimikib=10531 /
bimikif=10532 /
bimikik=10533 /
bimikil=10534 /
bimikim=10535 /
bimikip=10536 /
bimikir=10537 /
bimikis=10538 /
bimikit=10539 /
bimiliv=10540
bimilib=10541 /
bimilif=10542 /
bimilik=10543 /
bimilil=10544 /
bimilim=10545 /
bimilip=10546 /
bimilir=10547 /
bimilis=10548 /
bimilit=10549 /
bimimiv=10550
bimimib=10551 /
bimimif=10552 /
bimimik=10553 /
bimimil=10554 /
bimimim=10555 /
bimimip=10556 /
bimimir=10557 /
bimimis=10558 /
bimimit=10559 /
bimipiv=10560
bimipib=10561 /
bimipif=10562 /
bimipik=10563 /
bimipil=10564 /
bimipim=10565 /
bimipip=10566 /
bimipir=10567 /
bimipis=10568 /
bimipit=10569 /
bimiriv=10570
bimirib=10571 /
bimirif=10572 /
bimirik=10573 /
bimiril=10574 /
bimirim=10575 /
bimirip=10576 /
bimirir=10577 /
bimiris=10578 /
bimirit=10579 /
bimisiv=10580
bimisib=10581 /
bimisif=10582 /
bimisik=10583 /
bimisil=10584 /
bimisim=10585 /
bimisip=10586 /
bimisir=10587 /
bimisis=10588 /
bimisit=10589 /
bimitiv=10590
bimitib=10591 /
bimitif=10592 /
bimitik=10593 /
bimitil=10594 /
bimitim=10595 /
bimitip=10596 /
bimitir=10597 /
bimitis=10598 /
bimitit=10599 /
bipiviv=10600
bipivib=10601 /
bipivif=10602 /
bipivik=10603 /
bipivil=10604 /
bipivim=10605 /
bipivip=10606 /
bipivir=10607 /
bipivis=10608 /
bipivit=10609 /
bipibiv=10610
bipibib=10611 /
bipibif=10612 /
bipibik=10613 /
bipibil=10614 /
bipibim=10615 /
bipibip=10616 /
bipibir=10617 /
bipibis=10618 /
bipibit=10619 /
bipifiv=10620
bipifib=10621 /
bipifif=10622 /
bipifik=10623 /
bipifil=10624 /
bipifim=10625 /
bipifip=10626 /
bipifir=10627 /
bipifis=10628 /
bipifit=10628 /
bipikiv=10630
bipikib=10631 /
bipikif=10632 /
bipikik=10633 /
bipikil=10634 /
bipikim=10635 /
bipikip=10636 /
bipikir=10637 /
bipikis=10638 /
bipikit=10639 /
bipiliv=10640
bipilib=10641 /
bipilif=10642 /
bipilik=10643 /
bipilil=10644 /
bipilim=10645 /
bipilip=10646 /
bipilir=10647 /
bipilis=10648 /
bipilit=10649 /
bipimiv=10650
bipimib=10651 /
bipimif=10652 /
bipimik=10653 /
bipimil=10654 /
bipimim=10655 /
bipimip=10656 /
bipimir=10657 /
bipimis=10658 /
bipimit=10659 /
bipipiv=10660
bipipib=10661 /
bipipif=10662 /
bipipik=10663 /
bipipil=10664 /
bipipim=10665 /
bipipip=10666 /
bipipir=10667 /
bipipis=10668 /
bipipit=10669 /
bipiriv=10670
bipirib=10671 /
bipirif=10672 /
bipirik=10673 /
bipiril=10674 /
bipirim=10675 /
bipirip=10676 /
bipirir=10677 /
bipiris=10678 /
bipirit=10679 /
bipisiv=10680
bipisib=10681 /
bipisif=10682 /
bipisik=10683 /
bipisil=10684 /
bipisim=10685 /
bipisip=10686 /
bipisir=10687 /
bipisis=10688 /
bipisit=10689 /
bipitiv=10690
bipitib=10691 /
bipitif=10692 /
bipitik=10693 /
bipitil=10694 /
bipitim=10695 /
bipitip=10696 /
bipitir=10697 /
bipitis=10698 /
bipitit=10699 /
biriviv=10700
birivib=10701 /
birivif=10702 /
birivik=10703 /
birivil=10704 /
birivim=10705 /
birivip=10706 /
birivir=10707 /
birivis=10708 /
birivit=10709 /
biriviv=10710
biribib=10711 /
biribif=10712 /
biribik=10713 /
biribil=10714 /
biribim=10715 /
biribip=10716 /
biribir=10717 /
biribis=10718 /
biribit=10719 /
birifiv=10720
birifib=10721 /
birifif=10722 /
birifik=10723 /
birifil=10724 /
birifim=10725 /
birifip=10726 /
birifir=10727 /
birifis=10728 /
birifit=10728 /
birikiv=10730
birikib=10731 /
birikif=10732 /
birikik=10733 /
birikil=10734 /
birikim=10735 /
birikip=10736 /
birikir=10737 /
birikis=10738 /
birikit=10739 /
biriliv=10740
birilib=10741 /
birilif=10742 /
birilik=10743 /
birilil=10744 /
birilim=10745 /
birilip=10746 /
birilir=10747 /
birilis=10748 /
birilit=10749 /
birimiv=10750
birimib=10751 /
birimif=10752 /
birimik=10753 /
birimil=10754 /
birimim=10755 /
birimip=10756 /
birimir=10757 /
birimis=10758 /
birimit=10759 /
biripiv=10760
biripib=10761 /
biripif=10762 /
biripik=10763 /
biripil=10764 /
biripim=10765 /
biripip=10766 /
biripir=10767 /
biripis=10768 /
biripit=10769 /
biririv=10770
biririb=10771 /
biririf=10772 /
biririk=10773 /
biriril=10774 /
biririm=10775 /
biririp=10776 /
biririr=10777 /
biriris=10778 /
biririt=10779 /
birisiv=10780
birisib=10781 /
birisif=10782 /
birisik=10783 /
birisil=10784 /
birisim=10785 /
birisip=10786 /
birisir=10787 /
birisis=10788 /
birisit=10789 /
biritiv=10790
biritib=10791 /
biritif=10792 /
biritik=10793 /
biritil=10794 /
biritim=10795 /
biritip=10796 /
biritir=10797 /
biritis=10798 /
biritit=10799 /
bisiviv=10800
bisivib=10801 /
bisivif=10802 /
bisivik=10803 /
bisivil=10804 /
bisivim=10805 /
bisivip=10806 /
bisivir=10807 /
bisivis=10808 /
bisivit=10809 /
bisiviv=10810
bisibib=10811 /
bisibif=10812 /
bisibik=10813 /
bisibil=10814 /
bisibim=10815 /
bisibip=10816 /
bisibir=10817 /
bisibis=10818 /
bisibit=10819 /
bisifiv=10820
bisifib=10821 /
bisifif=10822 /
bisifik=10823 /
bisifil=10824 /
bisifim=10825 /
bisifip=10826 /
bisifir=10827 /
bisifis=10828 /
bisifit=10828 /
bisikiv=10830
bisikib=10831 /
bisikif=10832 /
bisikik=10833 /
bisikil=10834 /
bisikim=10835 /
bisikip=10836 /
bisikir=10837 /
bisikis=10838 /
bisikit=10839 /
bisiliv=10840
bisilib=10841 /
bisilif=10842 /
bisilik=10843 /
bisilil=10844 /
bisilim=10845 /
bisilip=10846 /
bisilir=10847 /
bisilis=10848 /
bisilit=10849 /
bisimiv=10850
bisimib=10851 /
bisimif=10852 /
bisimik=10853 /
bisimil=10854 /
bisimim=10855 /
bisimip=10856 /
bisimir=10857 /
bisimis=10858 /
bisimit=10859 /
bisipiv=10860
bisipib=10861 /
bisipif=10862 /
bisipik=10863 /
bisipil=10864 /
bisipim=10865 /
bisipip=10866 /
bisipir=10867 /
bisipis=10868 /
bisipit=10869 /
bisiriv=10870
bisirib=10871 /
bisirif=10872 /
bisirik=10873 /
bisiril=10874 /
bisirim=10875 /
bisirip=10876 /
bisirir=10877 /
bisiris=10878 /
bisirit=10879 /
bisisiv=10880
bisisib=10881 /
bisisif=10882 /
bisisik=10883 /
bisisil=10884 /
bisisim=10885 /
bisisip=10886 /
bisisir=10887 /
bisisis=10888 /
bisisit=10889 /
bisitiv=10890
bisitib=10891 /
bisitif=10892 /
bisitik=10893 /
bisitil=10894 /
bisitim=10895 /
bisitip=10896 /
bisitir=10897 /
bisitis=10898 /
bisitit=10899 /
bitiviv=10900
bitivib=10901 /
bitivif=10902 /
bitivik=10903 /
bitivil=10904 /
bitivim=10905 /
bitivip=10906 /
bitivir=10907 /
bitivis=10908 /
bitivit=10909 /
bitibiv=10910
bitibib=10911 /
bitibif=10912 /
bitibik=10913 /
bitibil=10914 /
bitibim=10915 /
bitibip=10916 /
bitibir=10917 /
bitibis=10918 /
bitibit=10919 /
bitifiv=10920
bitifib=10921 /
bitifif=10922 /
bitifik=10923 /
bitifil=10924 /
bitifim=10925 /
bitifip=10926 /
bitifir=10927 /
bitifis=10928 /
bitifit=10928 /
bitikiv=10930
bitikib=10931 /
bitikif=10932 /
bitikik=10933 /
bitikil=10934 /
bitikim=10935 /
bitikip=10936 /
bitikir=10937 /
bitikis=10938 /
bitikit=10939 /
bitiliv=10940
bitilib=10941 /
bitilif=10942 /
bitilik=10943 /
bitilil=10944 /
bitilim=10945 /
bitilip=10946 /
bitilir=10947 /
bitilis=10948 /
bitilit=10949 /
bitimiv=10950
bitimib=10951 /
bitimif=10952 /
bitimik=10953 /
bitimil=10954 /
bitimim=10955 /
bitimip=10956 /
bitimir=10957 /
bitimis=10958 /
bitimit=10959 /
bitipiv=10960
bitipib=10961 /
bitipif=10962 /
bitipik=10963 /
bitipil=10964 /
bitipim=10965 /
bitipip=10966 /
bitipir=10967 /
bitipis=10968 /
bitipit=10969 /
bitiriv=10970
bitirib=10971 /
bitirif=10972 /
bitirik=10973 /
bitiril=10974 /
bitirim=10975 /
bitirip=10976 /
bitirir=10977 /
bitiris=10978 /
bitirit=10979 /
bitisiv=10980
bitisib=10981 /
bitisif=10982 /
bitisik=10983 /
bitisil=10984 /
bitisim=10985 /
bitisip=10986 /
bitisir=10987 /
bitisis=10988 /
bitisit=10989 /
bititiv=10990
bititib=10991 /
bititif=10992 /
bititik=10993 /
bititil=10994 /
bititim=10995 /
bititip=10996 /
bititir=10997 /
bititis=10998 /
bititit=10999 /
bivaviv=101000 /
